Chứng tỏ rằng vật ở hình 6.11 sẽ cân bằng khi:
\(\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\)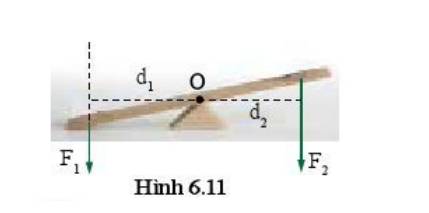
H24
Những câu hỏi liên quan
Chất điểm A chịu tác động của ba lực overrightarrow {{F_1}} ,;overrightarrow {{F_2}} ,;overrightarrow {{F_3}} như hình 4.30 và ở trạng thái cân bằng (tức là overrightarrow {{F_1}} + ;overrightarrow {{F_2}} + ;overrightarrow {{F_3}} overrightarrow 0 ). Tính độ lớn của các lực overrightarrow {{F_2}} ,;overrightarrow {{F_3}} biết overrightarrow {{F_1}} có độ lớn là 20N.
Đọc tiếp
Chất điểm A chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) như hình 4.30 và ở trạng thái cân bằng (tức là \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)). Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) biết \(\overrightarrow {{F_1}} \) có độ lớn là 20N.

Tham khảo:
Bước 1: Đặt \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.

Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \)
Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\;\overrightarrow u + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)
\( \Leftrightarrow \;\overrightarrow u \) và \(\;\overrightarrow {{F_3}} \) là hai vecto đối nhau.
\( \Leftrightarrow A\) là trung điểm của EC.
Bước 2:
Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC.\)
Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\)
\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3};\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}.\end{array} \right.\end{array}\)
Vậy \(\;\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3},\;\;\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}.\)
Đúng 0
Bình luận (0)
Chứng minh rằng: tam giác tạo bởi ba đường thẳng \(\left(d_1\right):y=3x-2;\left(d_2\right):y=-\dfrac{1}{3}x+\dfrac{4}{3};\left(d_3\right):y=-2x+8\) là tam giác vuông cân.
Bây giờ ta sẽ đi tìm tọa độ giao điểm của 3 đường thẳng trên
Với (d1) và (d2) cắt nhau tại điểm \(A\left(x_1;y_1\right)\) nên khi đó:
\(\hept{\begin{cases}y_1=3x_1-2\\y_1=-\frac{1}{3}x_1+\frac{4}{3}\end{cases}}\Rightarrow3x_1-2=-\frac{1}{3}x_1+\frac{4}{3}\Leftrightarrow\frac{10}{3}x_1=\frac{10}{3}\Rightarrow\hept{\begin{cases}x_1=1\\y_1=1\end{cases}}\)
Vậy \(A\left(1;1\right)\)
Tương tự gọi B,C là giao điểm của đường (d3) với (d2) , (d1)
Khi đó ta dễ dàng tính được: \(B\left(4;0\right)\) ; \(C\left(2;4\right)\)
Áp dụng công thức tính khoảng cách giữa 2 điểm trong mặt phẳng ta có:
\(AB=\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}=\sqrt{10}\Rightarrow AB^2=10\)
\(AC=\sqrt{\left(1-2\right)^2+\left(1-4\right)^2}=\sqrt{10}\Rightarrow AC^2=10\)
\(BC=\sqrt{\left(4-2\right)^2+\left(0-4\right)^2}=\sqrt{20}\Rightarrow BC^2=20\)
Xét tam giác ABC có: \(\hept{\begin{cases}AB=AC\\AB^2+AC^2=BC^2\left(=20\right)\end{cases}}\)
=> Tam giác ABC vuông cân tại A
=> đpcm
giao điểm của d1 với d2 là : y=3x-2
y=-1/3x+4/3
<=> 3x -2 =-1/3+4/3
y=3x-2
<=> x=1
y=1
vaaky giao điểm của d1 và d2 có tọa độ A(1,1)
tương tự ta được giao điểm của: d2 với d3 có tọa độ B (4,0)
d3 với d1 có tọa độ C(2,4)
độ dài AB là\(\sqrt{\left(Xa-Xb\right)^2+\left(Ya+Yb\right)^2}\)=\(\sqrt{\left(1-4\right)^2+\left(1-0\right)^2}\)=\(\sqrt{10}\)
tương tư ta được AC= \(\sqrt{10}\)
=> AB=AC ; d1 vuông góc d2 vì 3.(-1/3)=-1
=> tam giác ABC VUÔNG CÂN
Ta có:d1=d2 <=>3x-2=-1
Xem thêm câu trả lời
trong một máy nén thủy lực, gọi F1,F2 lần lượt là lực tác dụng lên pít tông lớn, nhỏ; S1, S2 lần lượt là diện tích pít tông lớn, nhỏ thì biểu thức nào sau đây đúng:A.dfrac{F_1}{F_2}dfrac{S_1}{S_2}B.dfrac{F_1}{F_2}dfrac{S_2}{S_1}C.dfrac{F_1}{S_2}dfrac{F_1}{S_1}D.F_1F_2.dfrac{S_2}{S_1}
Đọc tiếp
trong một máy nén thủy lực, gọi F1,F2 lần lượt là lực tác dụng lên pít tông lớn, nhỏ; S1, S2 lần lượt là diện tích pít tông lớn, nhỏ thì biểu thức nào sau đây đúng:
A.\(\dfrac{F_1}{F_2}=\dfrac{S_1}{S_2}\)
B.\(\dfrac{F_1}{F_2}=\dfrac{S_2}{S_1}\)
C.\(\dfrac{F_1}{S_2}=\dfrac{F_1}{S_1}\)
D.\(F_1=F_2.\dfrac{S_2}{S_1}\)
Gọi \(d_1< d_2< d_3< ...< d_k\) là tất cả các ước dương của 5292. Tính giá trị của tổng:
\(S=\dfrac{1}{\sqrt{d_1}+\sqrt{5292}}+\dfrac{1}{\sqrt{d_2}+\sqrt{5292}}+...+\dfrac{1}{\sqrt{d_k}+\sqrt{5292}}\)
chứng tỏ rằng với mọi n thuộc N ta luôn có
\(\dfrac{1}{1.6}+\dfrac{1}{6.11}+\dfrac{1}{11.16}+....+\dfrac{1}{\left(5n+1\right).\left(5n+6\right)}=\dfrac{n+1}{5n+6}\)
\(VT=\dfrac{1}{5}\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{\left(5n+1\right)\left(5n+6\right)}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+\dfrac{1}{11}-...+\dfrac{1}{5n+1}-\dfrac{1}{5n+6}\right)\)
\(=\dfrac{1}{5}\left(1-\dfrac{1}{5n+6}\right)\)
\(=\dfrac{1}{5}\cdot\dfrac{5n+6-1}{5n+6}\)
\(=\dfrac{n+1}{5n+6}=VP\)
Đúng 2
Bình luận (0)
Tính góc giữa các đường thẳng sau:
a) \(d_1:3x-4y=0\) và \(d_2:\left\{{}\begin{matrix}x=1+3t\\y=-4t\end{matrix}\right.\)
b) \(d_1:\dfrac{x}{1}=\dfrac{y+2}{-2}\) và \(d_2:\left\{{}\begin{matrix}x=5+3t\\t=1-t\end{matrix}\right.\)
Hai lực overrightarrow {{F_1}} ,overrightarrow {{F_2}} cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc (overrightarrow {{F_1}} ,overrightarrow {{F_2}} ) alpha làm cho vật di chuyển theo hướng từ O đến C (Hình 74). Lập công thức tính cường độ của hợp lực overrightarrow F làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực overrightarrow {{F_1}} ,overrightarrow {{F_2}} làm cho vật di chuyển).
Đọc tiếp
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cho trước cùng tác dụng lên một vật tại điểm O và tạo với nhau một góc \((\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = \alpha \) làm cho vật di chuyển theo hướng từ O đến C (Hình 74). Lập công thức tính cường độ của hợp lực \(\overrightarrow F \) làm cho vật di chuyển theo hướng từ O đến C (giả sử chỉ có đúng hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) làm cho vật di chuyển).
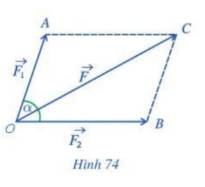
Ta có: \(\overrightarrow {{F_1}} = \overrightarrow {OA} ,\;\overrightarrow {{F_2}} = \overrightarrow {OB}= \overrightarrow {AC} \)
Khi đó: Hợp lực \(\overrightarrow F \) là \(\overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} \).
Áp dụng định lí cosin cho tam giác OAC, ta có:
\(\begin{array}{*{20}{l}}
{\;\;\;{\mkern 1mu} {\kern 1pt} \;O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos A}\\
\begin{array}{l}
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} - 2.OA.AC.\cos ({180^o} - \alpha )\\
\Leftrightarrow O{C^2} = O{A^2} + A{C^2} + 2.OA.AC.\cos \alpha
\end{array}\\
{ \Leftrightarrow \left| {\vec F} \right| = \sqrt {{{\left| {\overrightarrow {{F_1}} } \right|}^2} + {{\left| {\overrightarrow {{F_2}} } \right|}^2} + 2.\left| {\overrightarrow {{F_1}} } \right|.\left| {\overrightarrow {{F_2}} } \right|.\cos \alpha } }
\end{array}\)
Đúng 1
Bình luận (0)
Cho đường thẳng \(d_1:x-2y-3=0,d_2x+y+1=0.\) Xác định M\(\in\)\(d_1\)sao cho khoảng cách từ M đến đường thằng \(d_2\)bằng \(\dfrac{1}{\sqrt{2}}\)
Lời giải:
$M\in d_1$ nên gọi tọa độ của $M$ là $(2a+3,a)$
Khoảng cách từ $M$ đến $(d_2)$ là:\(\frac{|2a+3+a+1|}{\sqrt{1^2+1^2}}=\frac{1}{\sqrt{2}}\Leftrightarrow |3a+4|=1\Leftrightarrow 3a+4=\pm 1\)
\(\Leftrightarrow a=-1; a=\frac{-5}{3}\)
Thay vào ta có tọa độ của điểm $M$
Đúng 2
Bình luận (0)
Lấy \(M\in d_1\Rightarrow M\left(2y+3;y\right)\)
Ta có: \(d\left(M;d_2\right)=\dfrac{1}{\sqrt{2}}\Leftrightarrow\dfrac{\left|2y+3+y+1\right|}{\sqrt{1^2+1^2}}=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\dfrac{\left|3y+4\right|}{\sqrt{2}}=\dfrac{1}{\sqrt{2}}\Leftrightarrow\left|3y+4\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}3y+4=1\\3y+4=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-\dfrac{5}{3}\end{matrix}\right.\)
\(y=1\Rightarrow M\left(5;1\right)\)
\(y=-\dfrac{5}{3}\Rightarrow M\left(-\dfrac{1}{3};-\dfrac{5}{3}\right)\)
Đúng 1
Bình luận (1)
Hình 4.19 biểu diễn hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 3\;N,\;\left| {\overrightarrow {{F_2}} } \right| = 2\;N.\) Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \).
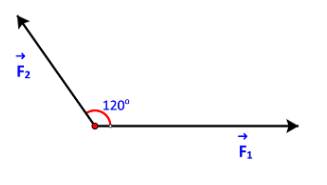
Tham khảo:
Dựng hình bình hành ABCD với hai cạnh là hai vectơ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) như hình vẽ
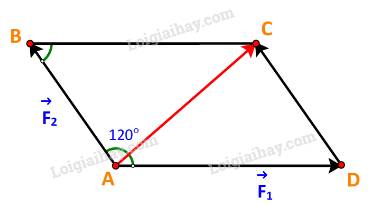
Ta có:
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {AD} + \overrightarrow {AB} = \overrightarrow {AC} \Rightarrow \left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {AC} } \right| = AC\)
Xét \(\Delta ABC\) ta có:
\(BC = AD = \left| {\overrightarrow {{F_1}} } \right| = 3\;,AB = \;\left| {\overrightarrow {{F_2}} } \right| = 2\;.\)
\(\widehat {ABC} = {180^o} - \widehat {BAD} = {180^o} - {120^o} = {60^o}\)
Theo định lí cosin ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\\ \Leftrightarrow A{C^2} = {2^2} + {3^2} - 2.2.3.\cos {60^o}\\ \Leftrightarrow A{C^2} = 7\\ \Leftrightarrow AC = \sqrt {7} \end{array}\)
Vậy \(\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \sqrt {7} \)
Đúng 0
Bình luận (0)








