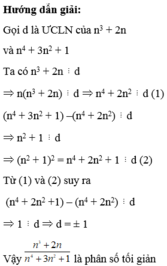Chứng minh rằng: n2+2/n4+3n2+1 tối giản
BN
Những câu hỏi liên quan
Chứng minh rằng với mọi số nguyên n thì phân số n 3 + 2 n n 4 + 3 n 2 + 1 là phân số tối giản
Chứng minh rằng với mọi số tự nhiên lẻ n:
1. n2 + 4n + 8 chia hết cho 8
2. n3 + 3n2 - n - 3 chia hết cho 48
a.
Đề bài sai, ví dụ \(n=1\) lẻ nhưng \(1^2+4.1+8=13\) ko chia hết cho 8
b.
n lẻ \(\Rightarrow n=2k+1\)
\(n^3+3n^2-n-3=n^2\left(n+3\right)-\left(n+3\right)=\left(n^2-1\right)\left(n+3\right)=\left(n-1\right)\left(n+1\right)\left(n+3\right)\)
\(=\left(2k+1-1\right)\left(2k+1+1\right)\left(2k+1+3\right)\)
\(=8k\left(k+1\right)\left(k+2\right)\)
Do \(k\left(k+1\right)\left(k+2\right)\) là tích 3 số tự nhiên liên tiếp nên chia hết cho 6
\(\Rightarrow8k\left(k+1\right)\left(k+2\right)\) chia hết cho 48
Đúng 1
Bình luận (0)
7. Chứng minh rằng với mọi số tự nhiên lẻ n:
n2+ 4n + 8 chia hết cho 8
n3+ 3n2- n - 3 chia hết cho 48
8. Tìm tất cả các số tự nhiên n để :
n4+ 4 là số nguyên tố
n1994+ n1993+ 1 là số nguyên tố
Chứng minh rằng phân số sau tối giản
\(\dfrac{2^{2024}+3}{2^{2023}+1}\) tối giản
Lời giải:
Gọi $d$ là ƯCLN $(2^{2024}+3, 2^{2023}+1)$
Ta có:
$2^{2024}+3\vdots d$
$2^{2023}+1\vdots d$
$\Rightarrow 2^{2024}+3-2(2^{2023}+1)\vdots d$
$\Rightarrow 1\vdots d$
$\Rightarrow d=1$
$\Rightarrow \frac{2^{2024+3}{2^{2023}+1}$ là ps tối giản.
Đúng 0
Bình luận (0)
Cho hình vẽ dưới đâya. Chứng minh rằng a // bb. Tính số đo
N
1
^
;
N
2
^
;
N
3
^
;
N
4
^
Đọc tiếp
Cho hình vẽ dưới đây
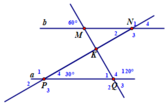 a. Chứng minh rằng a // b
a. Chứng minh rằng a // b
b. Tính số đo N 1 ^ ; N 2 ^ ; N 3 ^ ; N 4 ^
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °
Đúng 0
Bình luận (0)
1.
chứng minh rằng phân số a/a+1 là phân số tối giản (a thuộc Z)
2.
chứng minh rằng phân số 246913579/123456790 là phân số tối giản.
3.
chứng minh rằng phân số 4n+8/2n+3 là phân số tối giản.
trả lời nhanh lên đi tôi nay mình phải đi học rồi
Chứng minh rằng các phân số sau tối giản
c)\(\dfrac{2^{2024}+3}{2^{2023}+1}\) tối giản
Lời giải:
Gọi $d$ là ƯCLN $(2^{2024}+3, 2^{2023}+1)$
Ta có:
$2^{2024}+3\vdots d$
$2^{2023}+1\vdots d$
$\Rightarrow 2^{2024}+3-2(2^{2023}+1)\vdots d$
$\Rightarrow 1\vdots d$
$\Rightarrow d=1$
$\Rightarrow \frac{2^{2024+3}{2^{2023}+1}$ là ps tối giản.
Đúng 0
Bình luận (0)
Cho x/y tối giản. Chứng minh rằng: x/y+1 tối giản
Chứng minh rằng 3n-2 trên 4n-3 là phân số tối giản
Cho a trên b là một phân số chưa tối giản. Chứng minh rằng các phân sau chưa tối giản
a) a trên a-b
b) 2a trên a-2b
chứng minh rằng 12n+1/30n+2 là phân số tối giản
Gọi d là ƯCLN ( 12n+1; 30n+2 )
=> 12n + 1 ⋮ d => 5.( 12n + 1 ) ⋮ d => 60n + 5 ⋮ d ( 1 )
=> 30n + 2 ⋮ d => 2.( 30n + 2 ) ⋮ d => 60n + 4 ⋮ d ( 2 )
Từ ( 1 ) và ( 2 ) => [ ( 60n + 5 ) - ( 60n + 4 ) ] ⋮ d
=> 1 ⋮ d => d = 1
Vì ƯCLN ( 12n + 1 ; 30n + 2 ) = 1 nên 12n+1/30n+2 là p/s tối giản
Đúng 0
Bình luận (0)
Gọi d là ước chung của 12n+1 và 30n+2 ta có:
5.(12n+1)-2.(30n+2)=60n+5-60n-4=1 chia hết cho d
Vậy d=1 nên 12n+1 và 30n+2 là hai số nguyên tố cùng nhau, do đó \(\frac{12n+1}{30n+2}\) là phân số tối giản
Đúng 0
Bình luận (0)