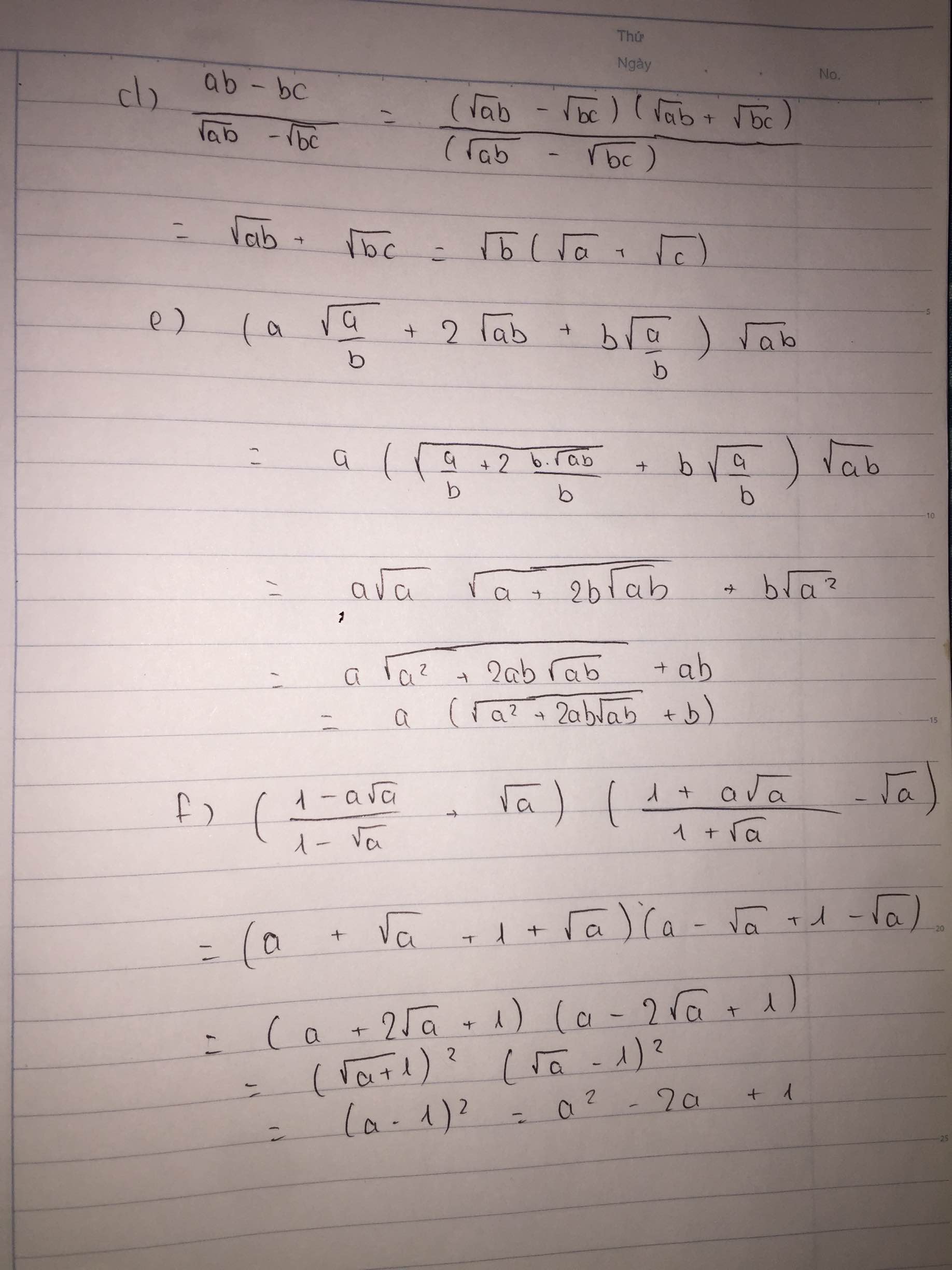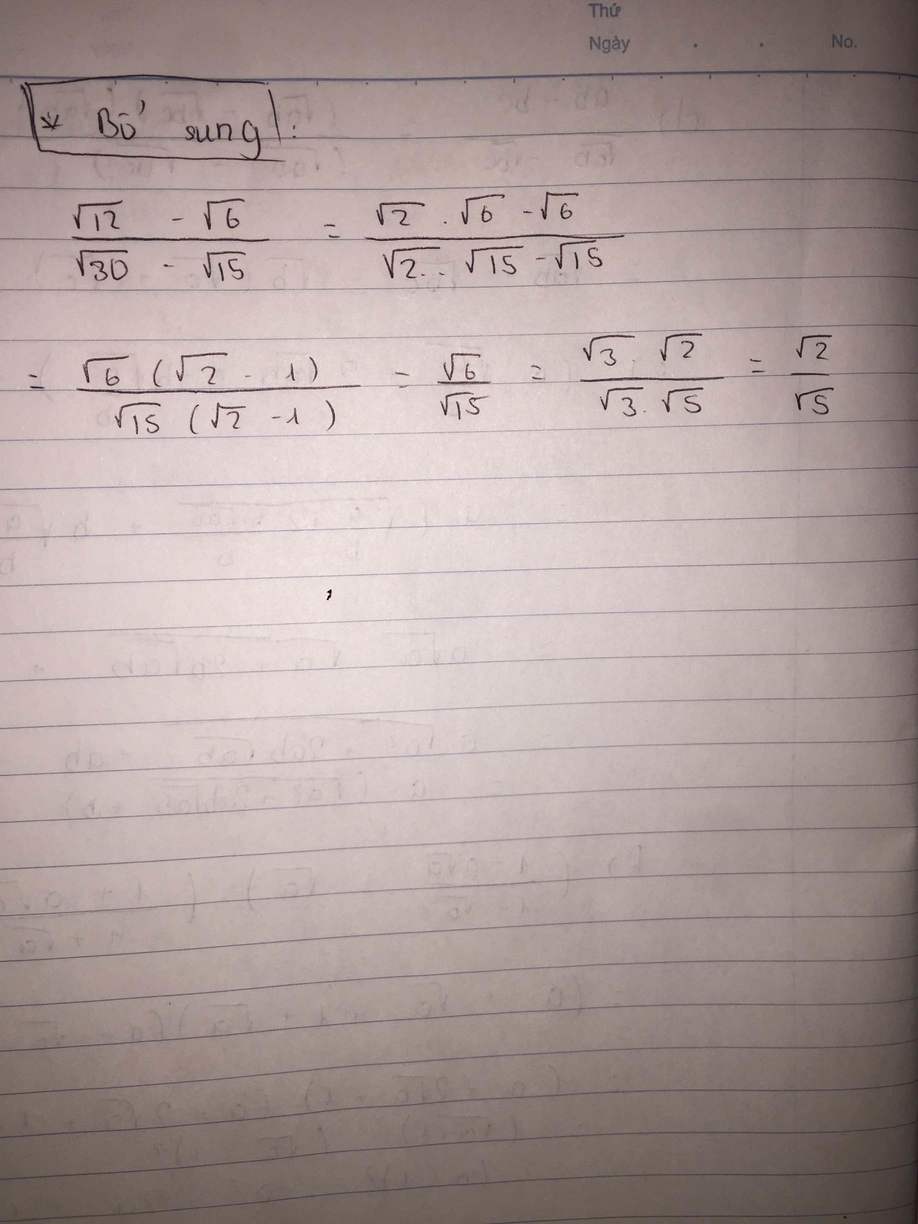Giusp e với ạ e cảm ơn ạ
DH
Những câu hỏi liên quan

Giusp e câu 2 với ạ
E đg cần gấp ạ, e cảm ơn nhiều
2. Thành phần biệt lập phụ chú (Dấu gạch ngang em nhé!)
Đúng 3
Bình luận (2)
 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)
Đúng 1
Bình luận (0)
Giusp em bài này với ạ. Em cảm ơn ạ.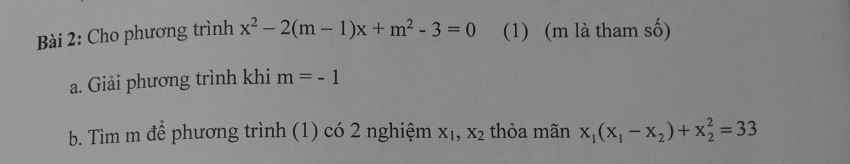
a.
Với \(m=-1\) pt trở thành: \(x^2+4x-2=0\)
\(\Delta'=4+2=6>0\) nên pt có 2 nghiệm pb:
\(x_1=-2+\sqrt{6}\) ; \(x_2=-2-\sqrt{6}\)
b.
\(\Delta'=\left(m-1\right)^2-\left(m^2-3\right)=-2m+4\ge0\Rightarrow m\le2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3\end{matrix}\right.\)
\(x_1\left(x_1-x_2\right)+x_2^2=33\)
\(\Leftrightarrow x_1^2+x_2^2-x_1x_2=33\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=33\)
\(\Leftrightarrow4\left(m-1\right)^2-3\left(m^2-3\right)=33\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10>2\left(loại\right)\\m=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho ABC vuông tại A. Lấy M bất kì trên cạnh BC . Gọi E,F lần lượt là các điểm đối xứng với M qua AB,AC.
a) Chứng minh A, E, F thẳng hàng.
b) Chứng minh A là trung điểm của EF.
làm giusp em vs ạ em cảm ơn.
Giusp em bài này với mọi người ạ, em cảm ơn rất nhiều ạ.

a.
Với \(m=3\) pt trở thành: \(2x^2+5x+2=0\)
\(\Delta=5^2-4.2.2=9>0\) nên pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{-5+\sqrt{9}}{2.2}=-\dfrac{1}{2}\)
\(x_2=\dfrac{-5-\sqrt{9}}{2.2}=-2\)
b.
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(4x_1^2+2x_1x_2+4x_2^2=1\)
\(\Leftrightarrow4\left(x_1^2+2x_1x_2+x_2^2\right)-6x_1x_2=1\)
\(\Leftrightarrow4\left(x_1+x_2\right)^2-6x_1x_2=1\)
\(\Leftrightarrow\left(2m-1\right)^2-3\left(m-1\right)=1\)
\(\Leftrightarrow4m^2-7m+3=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{3}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
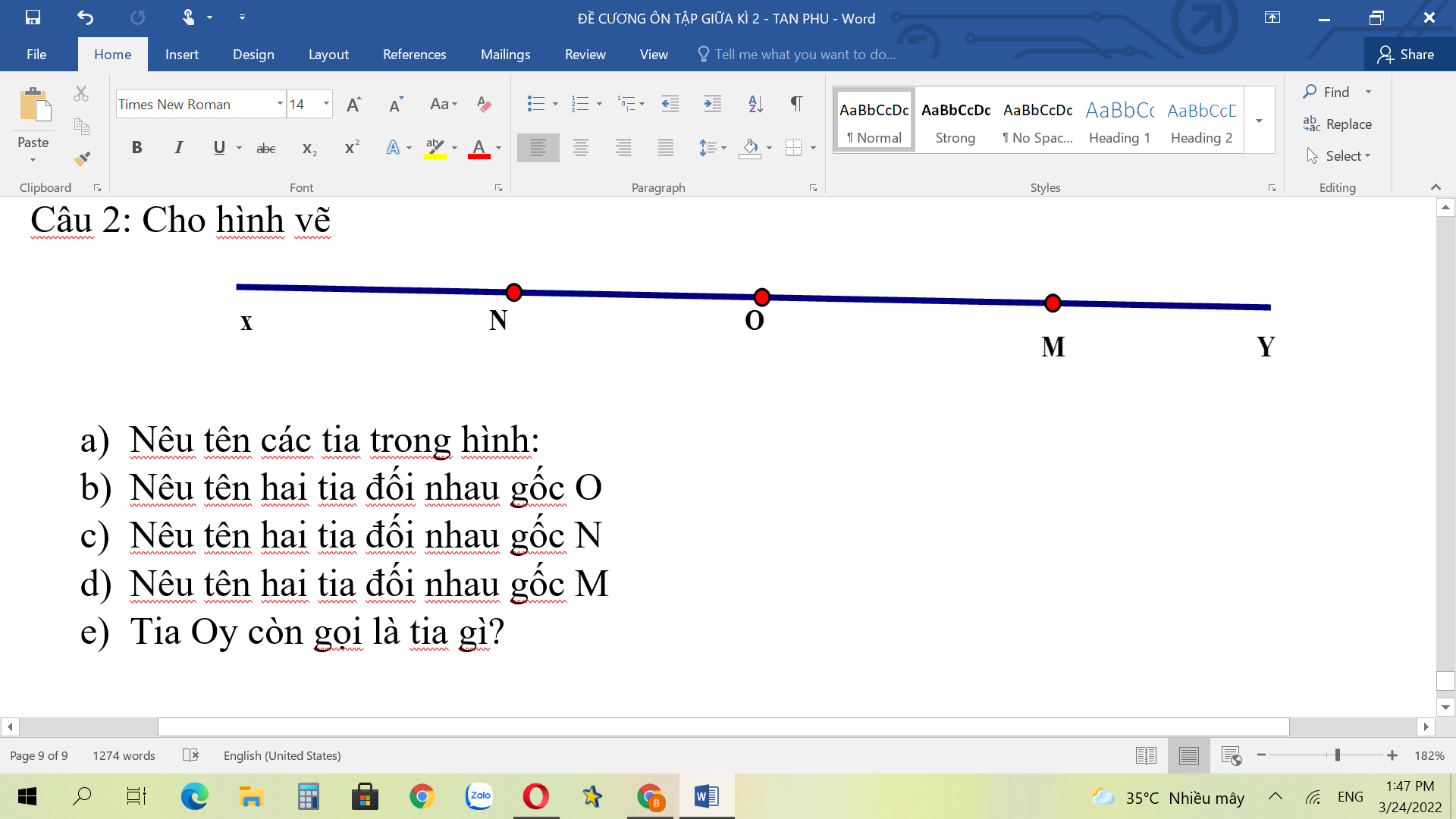
Giusp Mình với ạ ,mình cảm ơn nhiều
a: xN,xO,xO,xM,NO,NM,Nx,My,MO
b: ON và OM
c; NO và Nx
d: Mx và My
e: Còn gọi là tia OM
Đúng 0
Bình luận (0)
Giúp e với ạ e đang cần gấp ạ
E cảm ơn nhìu ạ 
đang thi mik ko giúp đc, xin lỗi nha
Đúng 0
Bình luận (10)
Giusp em với mng oiq! em cảm ơn rất nhiều ạ!!
a: Thay x=2 và y=0 vào (d), ta được:
-n+3+4=0
=>1-n=0
hay n=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+n-3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(n-3\right)=-4n+12+4=-4n+16\)
Để phương trình có hai nghiệm phân biệt thì -4n+16>0
hay n<4
Đúng 0
Bình luận (0)
Nung hoàn toàn hỗn hợp gồm CaCO3 và BaCO3 thu được 29,85 chất rắn và 5,6 lít khí ( ở ddktc ). Xác định % về khối lượng có trong hỗn hợp ban đầu.
Giusp e với e đang cần gấp. Cảm ơn ạ!!!!
\(n_{CO_2}=\dfrac{5,6}{22,4}=0,25\left(mol\right)\)
PTHH:
\(CaCO_3-t^o->CaO+CO_2\)
x.........................................x....................x
\(BaCO_3-t^o->BaO+CO_2\)
y........................................y.......................y
Gọi x, y lần lượt là số mol của \(CaCO_3;BaCO_3\)
Ta có hệ PT:
\(\left\{{}\begin{matrix}56x+153y=29,85\\x+y=0,25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0,09\\y=0,16\end{matrix}\right.\)
=> \(m_{CaCO_3}=0,09.100=9\left(g\right)\)
=> \(m_{BaCO_3}=0,16.197=31,52\left(g\right)\)
=> \(\left\{{}\begin{matrix}\%m_{CaCO_3}=\dfrac{9}{\left(9+31,52\right)}.100\%=22,21\%\\\%m_{BaCO_3}=100\%-22,21\%=77,79\%\end{matrix}\right.\)
Đúng 0
Bình luận (0)