giúp em câu 42-47 với ạ

mọi người ơi giúp em câu 42 với ạ 
Từ bảng biến thiên bạn có thể vẽ được đồ thị hàm số $f(x)$
Khi đó pt : $f(x)=\frac{2019}{2}$ có nghiệm duy nhất $x\in (3;+\infty)$
Đáp án D.
. Tính nhanh: a) (45×105-225)-(210+42×95) b) (47×105-235)-(168+42×96) Giúp với ạ. E đang cần gấp.
a) \(\left(45x105-225\right)-\left(210+42x95\right)\)
\(=45x\left(100+5\right)-225-210+42x\left(100-5\right)\)
\(=4500+45x5-225-210+4200-42x5\)
\(=4500+4200+45x5-42x5-225-210\)
\(=8700+5x\left(45-42\right)-435\)
\(=8700+15-435=8280\)
a: =45*105-225-210-42*95
=45*(105-5)-42(95+5)
=100*3
=300
b: =47(105-5)-42(96+4)
=47*100-42*100
=5*100
=500
b) \(\left(47x105-235\right)-\left(168+42x96\right)\)
\(=47x\left(100+5\right)-235-168-42x\left(100-4\right)\)
\(=4700+235-235-168-4200-168\)
\(=4700-4200+235-235-168-168\)
\(=500\)
ai Giúp em câu này nhanh với ạ
a) (3x+6)+(7y-14)=0
b) 17y+35+4x+17=42
e cảm ơn ạ
Giúp mình từ câu 42 đến câu 47
giúp e câu 47 này với ạ
GIÚP MÌNH CÂU 47 ĐẾN 50 VỚI Ạ!!
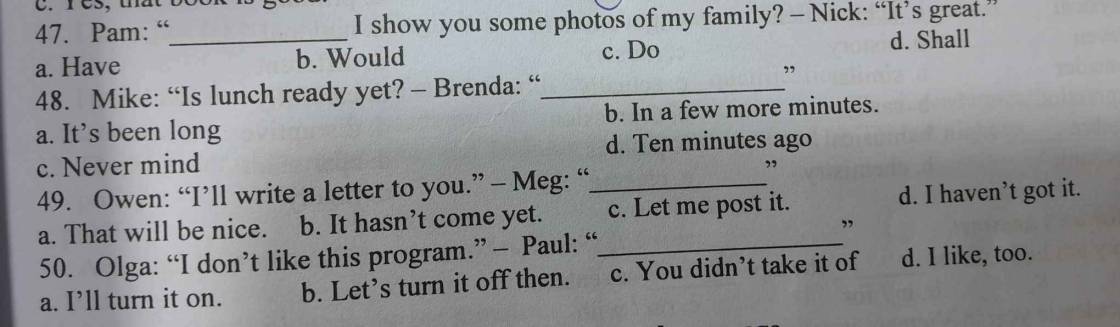
47 d
48 b
49 a
50 a
đây là theo suy nghĩ của mình thôi nên ko chắc nhé
GIÚP MÌNH TỪ CÂU 43 ĐẾN 47 VỚI Ạ

mọi người giúp em câu này ạ
x-[ 42+(- 28 ) = - x
\(\Leftrightarrow x-42+28=-x\\ \Leftrightarrow2x=14\Leftrightarrow x=7\)
MN có thể giúp em câu 41 và 42 đc ko ạ ?
41. Do \(\left(e;e^2\right)\in\left(2;+\infty\right)\) nên \(f\left(x\right)=3x^2+6x\)
\(I=\int\limits^{e^2}_e\dfrac{3\left(ln^2x\right)^2+6ln^2x}{x.lnx}dx=\int\limits^{e^2}_e\dfrac{3ln^3x+6lnx}{x}dx\)
Đặt \(lnx=t\Rightarrow\dfrac{dx}{x}=dt\) ; \(\left\{{}\begin{matrix}x=e\Rightarrow t=1\\x=e^2\Rightarrow t=2\end{matrix}\right.\)
\(I=\int\limits^2_1\left(3t^3+6t\right)dt=\int\limits^2_1\left(\dfrac{3}{4}t^4+3t^2\right)|^2_1=\dfrac{81}{4}\)
Cả 4 đáp án đều sai
42.
Đặt \(2021=a\) (ngắn cho dễ viết), \(z=x+yi\Rightarrow x^2+y^2=a^4\)
\(\left(x+\left(y+a\right)i\right)\left(x-\dfrac{1}{a}-yi\right)=x^2-\dfrac{x}{a}+y^2+ay+\left(ax-\dfrac{y}{a}-1\right)i\)
Số đã cho thuần ảo \(\Rightarrow\left\{{}\begin{matrix}x^2+y^2=a^4\\x^2+y^2-\dfrac{x}{a}+ay=0\end{matrix}\right.\) và \(ax-\dfrac{y}{a}-1\ne0\) (1)
\(\Rightarrow\left\{{}\begin{matrix}x^2+y^2=a^4\\a^4-\dfrac{x}{a}+ay=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x^2+y^2=a^4\\x=a^5+a^2y\end{matrix}\right.\)
\(\Rightarrow\left(a^5+a^2y\right)^2+y^2=a^4\)
\(\Rightarrow\left(a^4+1\right)y^2+2a^7y+a^{10}-a^4=0\)
\(\Delta'=a^{14}-\left(a^4+1\right)\left(a^{10}-a^4\right)=-a^4\left(a^6-a^4-1\right)< 0\)
\(\Rightarrow\) Pt vô nghiệm hay ko tồn tại số phức thỏa yêu cầu