Lập bảng xét dấu: f(x) = \(5x^2+4x-1\)
29
Những câu hỏi liên quan
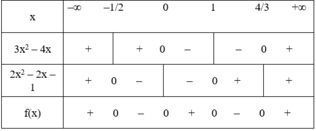
Lập bảng xét dấu biểu thức sau: f(x) = (3x2 - 4x)(2x2 - x - 1)
f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
Đúng 0
Bình luận (0)
Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
b) \(f\left( x \right) = {x^2} - x - 12\)
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
Tham khảo:
a) \(f\left( x \right) = - 3{x^2} + 4x - 1\)
\(a = - 3 < 0\), \(\Delta = {4^2} - 4.\left( { - 3} \right).\left( { - 1} \right) = 4 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = \frac{1}{3},x = 1\)
Bảng xét dấu:

b) \(f\left( x \right) = {x^2} - x - 12\)
\(a = 1 > 0\), \(\Delta = {\left( { - 1} \right)^2} - 4.1.\left( { - 12} \right) = 49 > 0\)
=> \(f\left( x \right)\) có 2 nghiệm \(x = - 3,x = 4\)
Bảng xét dấu:

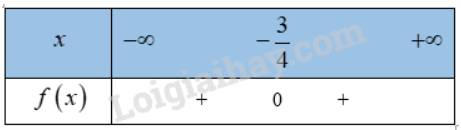
c) \(f\left( x \right) = 16{x^2} + 24x + 9\)
\(a = 16 > 0\), \(\Delta ' = {12^2} - 16.9 = 0\)
=> \(f\left( x \right)\) có nghiệm duy nhất \(x = - \frac{3}{4}\)
Bảng xét dấu:
Đúng 0
Bình luận (0)
Lập bảng xét dấu :
\(f\left(x\right)=-5x^2+2x+3\)
Ta có \(a=-5<0;\Delta'=16>0;x_1=-\frac{3}{5};x_2=1\)
Bảng xét dấu :
| \(x\) | \(-\infty\) \(-\frac{3}{5}\) 1 \(+\infty\) |
| \(f\left(x\right)\) | - 0 + - |
Từ bảng xét, ta được :
\(T\left(f\left(x\right)=0\right)=\left\{-\frac{3}{5};1\right\}\) ; \(T\left(f\left(x\right)\ne0\right)=R\)/ \(\left\{-\frac{3}{5};1\right\}\)
\(T\left(f\left(x\right)>0\right)=\left\{-\frac{3}{5};1\right\}\) ; \(T\left(f\left(x\right)\ge0\right)=\left[-\frac{3}{5};1\right]\)
Từ : \(T\left(f\left(x\right)<0\right)=\left(-\infty;-\frac{3}{5}\right)\cup\left(1;+\infty\right)\) ; \(T\left(f\left(x\right)\le0\right)=\left(-\infty;-\frac{3}{5}\right)\cup\left(1;+\infty\right)\)
Đúng 0
Bình luận (0)
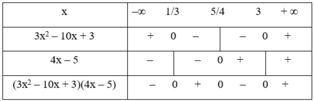
Lập bảng xét dấu biểu thức sau: f(x) = (3x2 - 10x + 3)(4x - 5)
f(x) = (3x2 – 10x + 3)(4x – 5)
+ Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3.
+ Nhị thức 4x – 5 có nghiệm x = 5/4.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)
f(x) = 0 khi x ∈ {1/3; 5/4; 3}
f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)
Đúng 0
Bình luận (0)
Lập bảng xét dấu (x-2)(-x2-x+2)
(x2-5x+6)(x2-10x+21)>=0
Xem chi tiết
Xét dấu các biểu thức sau:
a) f(x)= (x-2).(x+1)/3x -1
b) f(x)= 1-4x /2x-3
c) f(x)= 3x (6 -2x)/5x-4
d) f(x)= -4/3x+1 - 3/2-x
e) f(x)= 2x-5/(3x+1) (2-4x)
Xem chi tiết
Lập bảng xét dấu
\(f\left(x\right)=x^2-x+1\)
Có a=1>0; \(\Delta=-3<0\)
Bảng xét dấu :
| x | \(-\infty\) \(+\infty\) |
| \(f\left(x\right)\) | + |
Từ bảng xét dấu trên, ta được :
\(T\left(f\left(x\right)=0\right)=\varnothing;T\left(f\left(x\right)\ne0\right)=R;T\left(f\left(x\right)>0\right)=R;T\left(f\left(x\right)\ge0\right)=R\)
\(T\left(f\left(x\right)<0\right)=\varnothing;T\left(f\left(x\right)\le0\right)=\varnothing\)
Đúng 0
Bình luận (0)
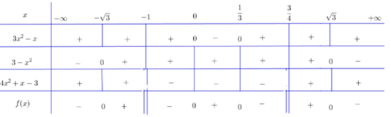
Lập bảng xét dấu biểu thức sau: f(x) = (4x2 - 1)(-8x2 + x - 3)(2x + 9)
f(x) = (4x2 – 1)(–8x2 + x – 3)(2x + 9)
+ Tam thức 4x2 – 1 có hai nghiệm x = –1/2 và x = 1/2, hệ số a = 4 > 0
Do đó 4x2 – 1 mang dấu + nếu x < –1/2 hoặc x > 1/2 và mang dấu – nếu –1/2 < x < 1/2
+ Tam thức –8x2 + x – 3 có Δ = –95 < 0, hệ số a = –8 < 0 nên luôn mang dấu –.
+ Nhị thức 2x + 9 có nghiệm x = –9/2.
Ta có bảng xét dấu:
Kết luận:
f(x) > 0 khi x ∈ (–∞; –9/2) ∪ (–1/2; 1/2)
f(x) = 0 khi x ∈ {–9/2; –1/2; 1/2}
f(x) < 0 khi x ∈ (–9/2; –1/2) ∪ (1/2; +∞)
Đúng 0
Bình luận (0)
Lập bảng xét dấu f'(x) biết f(x) = |x2 - 2x - 3|




