tích của 2 số là 7500 biết S1=3/4 S2.Tìm S2
LC
Những câu hỏi liên quan
Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a có diện tích xung quanh là
S
1
và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích là
S
2
. Khi đó, hệ thức giữa
S
1
và
S
2
là:A.
S...
Đọc tiếp
Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a có diện tích xung quanh là S 1 và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích là S 2 . Khi đó, hệ thức giữa S 1 và S 2 là:
A. S 1 = S 2 B. S 1 = 4 S 2
C. S 2 = 2 S 1 D. 2 S 2 = 3 S 1
Chọn D.
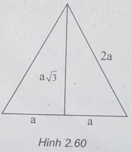
(h.2.60) Bán kính đáy của hình nón là a, đường sinh của hình nón là 2a.
Do đó, ta có:
S 1 = π Rl = π .a.2a = 2 πa 2 (1)
Mặt cầu có bán kính là a 3 /2, nên ta có:
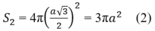
Từ (1) và (2) suy ra: 2 S 2 = 3 S 1
Đúng 0
Bình luận (0)
Cho hàm số
y
x
2
-
m
x
(
0
m
4
)
có đồ thị (C). Gọi
S
1
là diện tích hình phẳng giới hạn bởi (C) và trục hoành;
S
2
là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng xm,x4. Biết
S
1...
Đọc tiếp
Cho hàm số y = x 2 - m x ( 0 < m < 4 ) có đồ thị (C). Gọi S 1 là diện tích hình phẳng giới hạn bởi (C) và trục hoành; S 2 là diện tích hình phẳng giới hạn bởi (C), trục hoành và hai đường thẳng x=m,x=4. Biết S 1 = S 2 , giá trị của m bằng
A. 10 3 .
B. 2.
C. 3.
D. 8 3 .
Bài 1: tìm x biết giá trị tuyệt đối của x lớn hơn hoặc bằng 25
Bài 2; tính S1 + S2 .Biết
S1=1+(-3)+5+(-7)+......+17
S2=(-2)+4+(-6)+8+.......+(-18)
Bài 1:
$|x|\geq 25\Rightarrow x\geq 25$ hoặc $x\leq -25$
Đúng 0
Bình luận (0)
Bài 2:
$S_1=1+[(-3)+5]+[(-7)+9]+...+[(-15)+17]$
$=1+2+2+....+2$
Số lần xuất hiện của 2 là: $[(17-3):2+1]:2=4$
$\Rightarrow S_1=1+2.4=9$
-------------------------
$S_2=(-2)+[4+(-6)]+[8+(-10)]+...+[16+(-18)]$
$=(-2)+(-2)+(-2)+...+(-2)$
Số lần xuất hiện của -2 là:
$[(18-4):2+1]:2+1=5$
$\Rightarrow S_2=(-2).5=-10$
$S_1+S_2=9+(-10)=-1$
Đúng 0
Bình luận (0)
Cho mặt cầu (S1) bán kính R1, mặt cầu (S2) bán kính R2 = 2R1 . Tìm tỉ số diện tích của mặt cầu (S2) và (S1).
\(S_{\left(S_1\right)}=4\pi R_1^2\)
\(S_{\left(S_2\right)}=4\pi R_2^2=4\pi\left(2R_1\right)^2=4.4\pi R_1^2\)
\(\Rightarrow\dfrac{S_{\left(S_2\right)}}{S_{\left(S_1\right)}}=4\)
Đúng 0
Bình luận (0)
Biết rằng parabol
y
1
24
x
2
chia hình phẳng giới hạn bởi elip có phương trình
x
2
16
+
y
2
1
1
thành hai phần có diện tích lần lượt
S
1
,
S
2
là với...
Đọc tiếp
Biết rằng parabol y = 1 24 x 2 chia hình phẳng giới hạn bởi elip có phương trình x 2 16 + y 2 1 = 1 thành hai phần có diện tích lần lượt S 1 , S 2 là với S 1 < S 2 . Tỉ số của S 1 S 2 bằng
A . 4 π + 3 8 π - 3
B . 4 π - 2 8 π + 2
C . 4 π + 3 12 π
D . 8 π - 3 12 π
Cấu hình electron của nguyên tố X là 1
s
2
2
s
2
2
p
6
3
s
2
3
p
6
4
s
1
. Vậy X có đặc điểm A. là nguyên tố thuộc chu kì 4, nhóm IA B. là nguyên tố cuối cùng của chu kì 4 C. là một kim loại có tính khử yếu D. tất cả đặc điểm trên đều đúng
Đọc tiếp
Cấu hình electron của nguyên tố X là 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 4 s 1 . Vậy X có đặc điểm
A. là nguyên tố thuộc chu kì 4, nhóm IA
B. là nguyên tố cuối cùng của chu kì 4
C. là một kim loại có tính khử yếu
D. tất cả đặc điểm trên đều đúng
Cho tam giác ABC có AB = AC.Các điểm D,E lần lượt trên cạnh AB , AC sao cho AD = CE.Gọi M là giao điểm của hai đoạn thẳng BE và CD.Gọi diện tích của hình tứ giác ADME là S1 diện tích của hình tam giác BCM là S2.
Tính tỉ số S1 : ( S2 x 2 + S1 x 3 )

Ta thấy tam giác ADC và tam giác ABC có chung chiều cao hạ từ đỉnh C nên \(\frac{S_{ADC}}{S_{ABC}}=\frac{AD}{AB}\)
Ta thấy tam giác BEC và tam giác BAC có chung chiều cao hạ từ đỉnh B nên \(\frac{S_{BEC}}{S_{BAC}}=\frac{CE}{AC}\)
Lại có AD = CE, AB = AC nên \(\frac{S_{ADC}}{S_{ABC}}=\frac{S_{BEC}}{S_{BAC}}\Rightarrow S_{ADC}=S_{BEC}\)
\(\Rightarrow S_{ADC}-S_{MEC}=S_{BEC}-S_{MEC}\Rightarrow S_{ADME}=S_{BMC}\Rightarrow S_1=S_2\)
Từ đó ta có: \(\frac{S_1}{S_2\times2+S_1\times3}=\frac{S_1}{S_1\times2+S_1\times3}=\frac{S_1}{S_1\times5}=\frac{1}{5}\)
Đúng 0
Bình luận (0)
Bài giải :

Ta thấy tam giác ADC và tam giác ABC có chung chiều cao hạ từ đỉnh C nên SADCSABC =ADAB
Ta thấy tam giác BEC và tam giác BAC có chung chiều cao hạ từ đỉnh B nên SBECSBAC =CEAC
Lại có AD = CE, AB = AC nên SADCSABC =SBECSBAC ⇒SADC=SBEC
⇒SADC−SMEC=SBEC−SMEC⇒SADME=SBMC⇒S1=S2
Từ đó ta có: S1S2×2+S1×3 =S1S1×2+S1×3 =S1S1×5 =15
Đúng 0
Bình luận (0)
Parabol
y
x
2
2
chia hình tròn có tâm là gốc tọa độ, bán kính bằng
2
2
thành hai phần có diện tích là
S
1
và
S
2
, trong đó
S
1
S
2
. Tìm tỉ số
S
1...
Đọc tiếp
Parabol y = x 2 2 chia hình tròn có tâm là gốc tọa độ, bán kính bằng 2 2 thành hai phần có diện tích là S 1 và S 2 , trong đó S 1 < S 2 . Tìm tỉ số S 1 S 2
A. 3 π + 2 21 π - 2
B. 3 π + 2 9 π - 2
C. 3 π + 2 12 π
D. 9 π - 2 3 π + 2
1. Một đường tròn và 1 hình vuông có cùng chu vi là 20 cm. Gọi S1 là diện tích hình tròn và S2 là diện tích hình vuông. Khẳng định nào sau đây đúng: A. S1 S2 B. S1 S2 C. S1 S2 D. S1 S2 + 22. Nếu a x b ( a - b ) : 2 thì giá trị của 2018 x 6 là: A. 2012 B. 1006 C. 1009 D. 20153. Một cửa hàng niêm yết giá bán một chiếc tivi là 13 400 000 đồng. Nếu bán chiếc tivi này...
Đọc tiếp
1. Một đường tròn và 1 hình vuông có cùng chu vi là 20 cm. Gọi S1 là diện tích hình tròn và S2 là diện tích hình vuông. Khẳng định nào sau đây đúng: A. S1 < S2 B. S1 > S2 C. S1 = S2 D. S1 = S2 + 2
2. Nếu a x b = ( a - b ) : 2 thì giá trị của 2018 x 6 là: A. 2012 B. 1006 C. 1009 D. 2015
3. Một cửa hàng niêm yết giá bán một chiếc tivi là 13 400 000 đồng. Nếu bán chiếc tivi này băng 50% giá niêm yết thì lãi 25% so với tiền vốn. Vậy tiền vón của chiếc tivi đó là: A. 6 700 00 đ B. 5 025 000 đ C. 4 020 000 đ D. 5 360 000 đ






