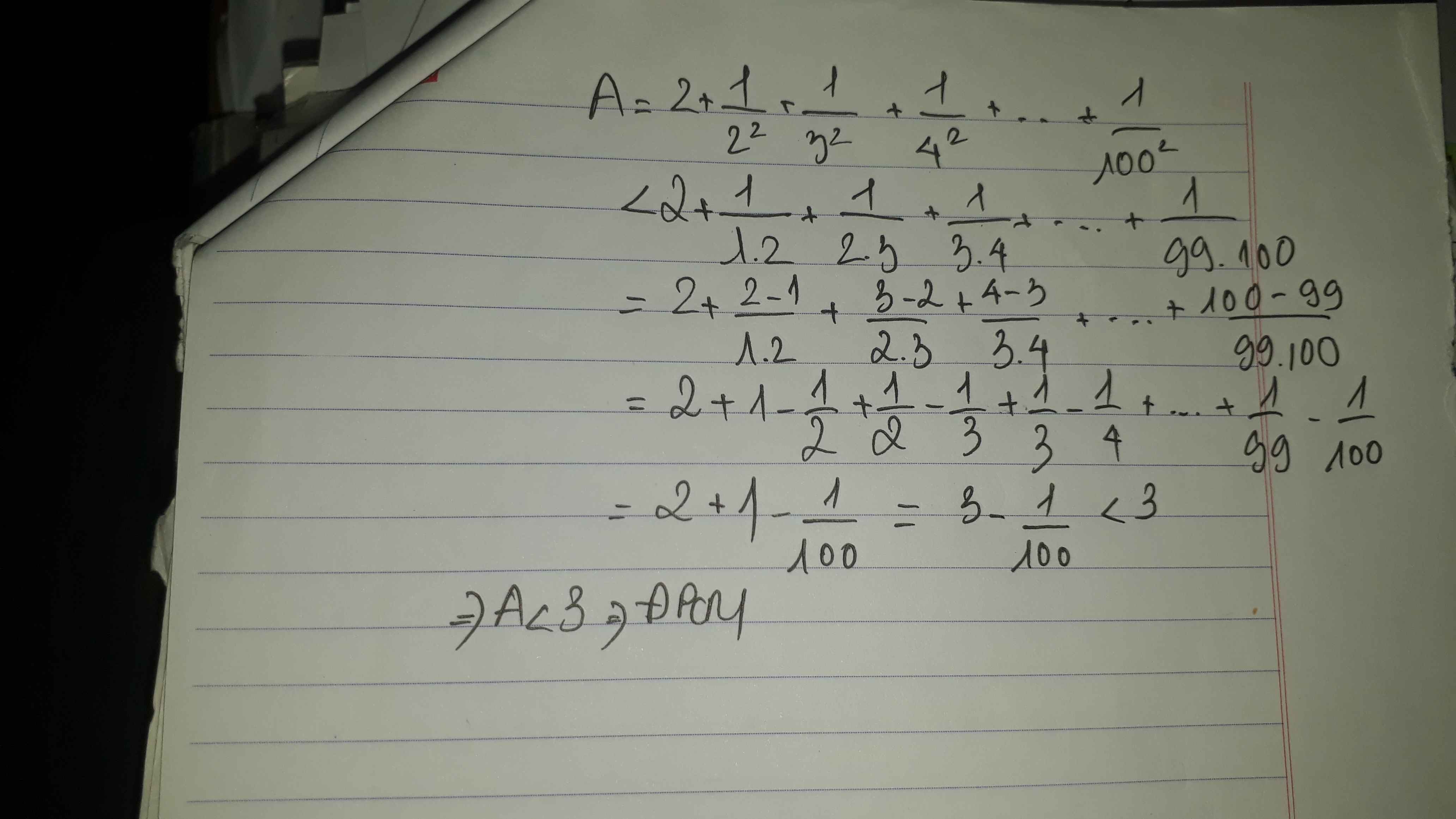chứng tỏ rằng 1/2^2 + 1/3^2 +...+1/100^2 <1
LN
Những câu hỏi liên quan
chứng tỏ rằng 1/2^2+1/3^2+...+1/100^2<3/4
chứng tỏ rằng:1/2^2+1/3^2+1/4^2+...+1/99^2+1/100^2<3/4
A=1*2-1/2! + 2*3-1/3! +....+ 99*100-1/100!
Chứng tỏ rằng A<1
Hãy chứng tỏ rằng : 100-[1+1/2+1/3+...+1/100] = 1/2+2/3+3/4+...+99/100
Mình cần gấp
Ta có : \(\frac{1}{2}+\frac{2}{3}+..+\frac{99}{100}\)
= \((1-\frac{1}{2})+(1-\frac{1}{3})+...+(1-\frac{99}{100})\)(100 cặp số )
= \(\left(1+1+1+...+1\right)-\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{100}\right)\)(100 số hạng 1)
= \(1\times100-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+..+\frac{1}{100}\right)\)
= \(100-\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{100}\right)\)
=> 100-(1+1/2+1/3+...+1/100) = 1/2+2/3+3/4+...+99/100
Đúng 3
Bình luận (0)
Bạn cố giải cho mình dễ hiểu hơn ko?
Đúng 0
Bình luận (0)
Cho A=1+1/2+1/3+1/4+...+1/2^100-1.Chứng tỏ rằng 50<A<100
chứng tỏ rằng 1/2^2+1/3^2+1/4^2+ ....+1/100^2<1
chứng tỏ rằng :1/2^2+1/3^2+1/4^2+...........+1/100^2<1
Co 1/2^2+1/3^2+...+1/100^2<1/1.2+1/2.3+...+1/99.100
=1-1/2+1/2-1/3+...+1/99-1/100
=1-1/100<1
vay 1/2^2+...+1/100^2<1
Đúng 0
Bình luận (0)
Bài 1:
a) Chứng tỏ rằng : 200 - (3+2/3+2/4+....+2/100)
--------------------------------------- = 2
1/2+2/3+3/4+....+9/100
b) Cho B =5/2.1 + 4/1.11 + 3/11.2 + 1/2.15 + 15/4.43 + 13/43
Chứng tỏ rằng B > 3
BB
18 tháng 7 2021 lúc 20:40
Chứng tỏ rằng: A= 2+\(\dfrac{1}{2^2}\)+\(\dfrac{1}{3^2}^{ }\)+\(\dfrac{1}{4^2}\)+...+\(\dfrac{1}{100^2}\)<3
