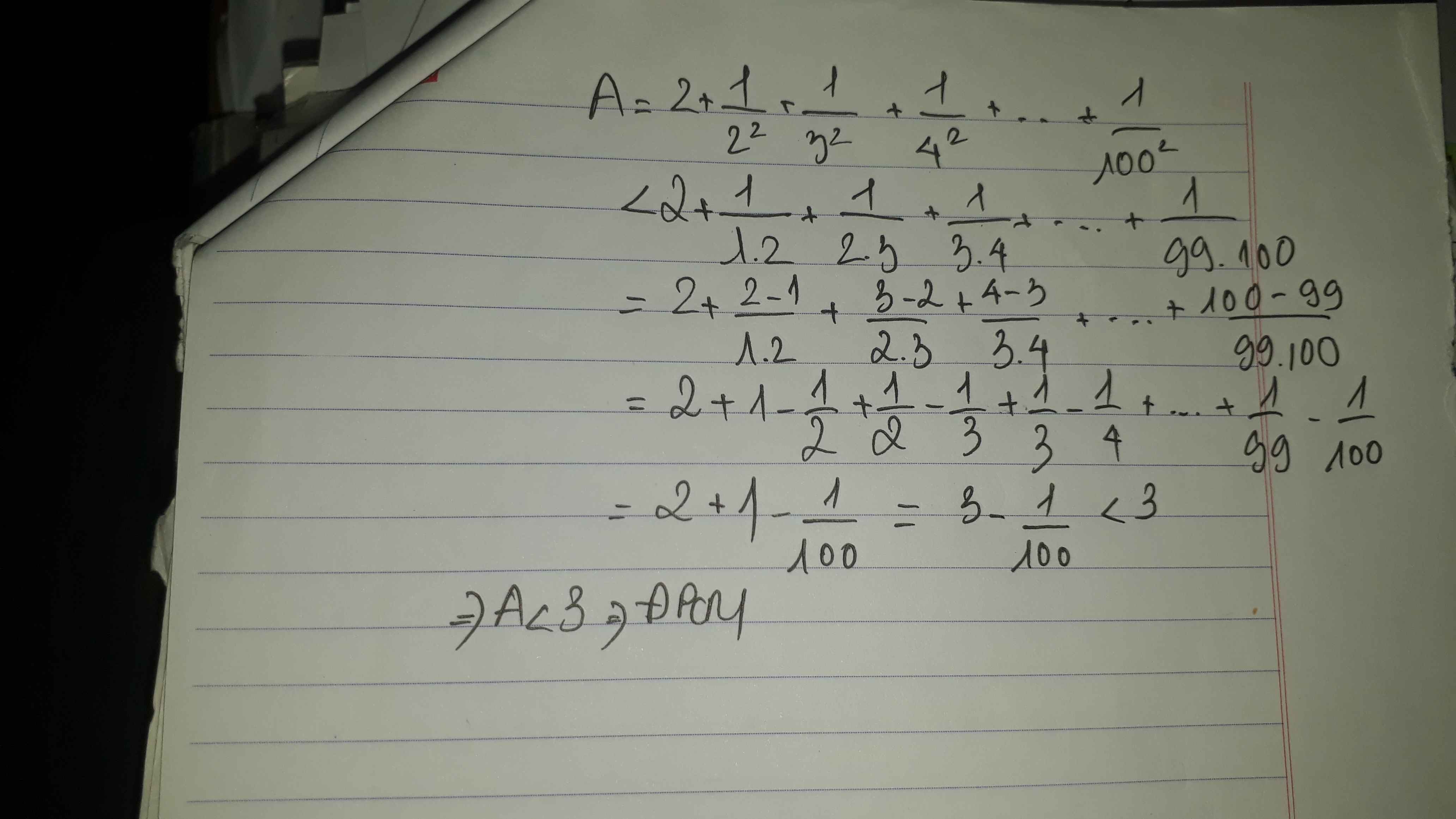BB
18 tháng 7 2021 lúc 20:40
Các câu hỏi tương tự
TQ
25 tháng 4 2023 lúc 9:53
Chứng tỏ rằng:
a)\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{3}{4}\)
b)\(\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}< \dfrac{1}{2}\)
chứng tỏ rằng:\(\dfrac{1}{2^2}\dfrac{1}{3^2}\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{3}{4}\)
cho em lời giải chi tiết với ạ
H24
11 tháng 4 2021 lúc 15:06
text{Bài 4. Chứng tỏ rằng:}a) dfrac{1}{2^2}+dfrac{1}{3^2}+dfrac{1}{4^2}+...+dfrac{1}{30^2} 1b) dfrac{1}{10}+dfrac{1}{11}+dfrac{1}{12}+...+dfrac{1}{99}+dfrac{1}{100}1c) dfrac{1}{5}+dfrac{1}{6}+dfrac{1}{7}+...+dfrac{1}{17} 2d) dfrac{1}{1.2}+dfrac{1}{2.3}+dfrac{1}{3.4}+...+dfrac{1}{29.30} 1
Đọc tiếp
\(\text{Bài 4. Chứng tỏ rằng:}\)
\(a\)) \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{30^2}< 1\)
\(b\)) \(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}+...+\dfrac{1}{99}+\dfrac{1}{100}>1\)
\(c\)) \(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+...+\dfrac{1}{17}< 2\)
\(d\)) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{29.30}< 1\)
Cho \(S=\dfrac{1}{5^2}+\dfrac{2}{5^3}+\dfrac{3}{5^4}+...+\dfrac{99}{5^{100}}\). Chứng tỏ rằng S<\(\dfrac{1}{16}\)
LQ
23 tháng 4 2023 lúc 15:20
Cho S=\(\dfrac{1}{5^2}+\dfrac{2}{5^3}+\dfrac{3}{5^4}+...+\dfrac{99}{5^{100}}\) . Chứng tỏ rằng \(S< \dfrac{1}{16}\)
KJ
18 tháng 2 2022 lúc 18:27
Cho F = \(\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}=\dfrac{1}{4^2}+...+\dfrac{1}{99^2}+\dfrac{1}{100^2}\). Chứng tỏ \(F< 1\dfrac{3}{4}\)
Chứng tỏ rằng: \(\dfrac{200-\left(3+\dfrac{2}{3}+\dfrac{2}{4}+\dfrac{2}{5}+...+\dfrac{2}{100}\right)}{\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+...+\dfrac{99}{100}}\)=2
LT
14 tháng 7 2021 lúc 18:39
Cho A = \(\dfrac{1}{2}\) + \(\dfrac{1}{2^{2}}\)+ \(\dfrac{1}{2^{3}}\)+ \(\dfrac{1}{2^{4}}\) + ...+ \(\dfrac{1}{2^{10}}\)
Chứng tỏ rằng A + \(\dfrac{1}{2^{10}}\)= 1
Chứng Minh Rằng : A= \(\dfrac{1}{2^2}\)+\(\dfrac{1}{3^2}\)+\(\dfrac{1}{4^2}\)+...+\(\dfrac{1}{100^2}\) <\(\dfrac{3}{4}\)