vẽ hình viết gt kt của định lý sau'' hai góc cùng phụ một góc thứ ba thì bằng nhau
AB
Những câu hỏi liên quan
Ta gọi hai góc có tổng bằng $90^{\circ}$ là hai góc phụ nhau. Vẽ hình, viết giả thiết, kết luận bằng kí hiệu định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
Giả thiết - Kết luận:
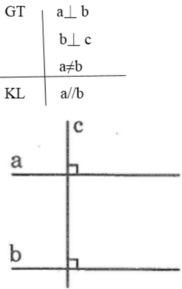
| GT |
|
| KL |
Đúng 0
Bình luận (0)
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
Giả thiết - Kết luận:
| GT |
|
| KL | |
Đúng 1
Bình luận (0)
A
B
C
O
D
GT:DOA+AOB=90
AOB+BOC=90
KL:DOA=BOC
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Vẽ hình họa, viết GT và KL của định lí :"Hai góc cùng bù với với một góc thứ ba thì hai góc đó bằng nhau".
| GT | \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau |
| KL | \(\widehat{CAB}=\widehat{GFE}\) |
Vì \(\widehat{CAD};\widehat{CAB}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{CAB}=180^0\)
=>\(\widehat{CAB}=180^0-\widehat{CAD}\left(1\right)\)
Vì \(\widehat{CAD};\widehat{GFE}\) là hai góc bù nhau
nên \(\widehat{CAD}+\widehat{GFE}=180^0\)
=>\(\widehat{GFE}=180^0-\widehat{CAD}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{CAB}=\widehat{GFE}\)
Đúng 0
Bình luận (0)
Vẽ hình và viết giả thiết, kết luận của các định lý sau: Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau
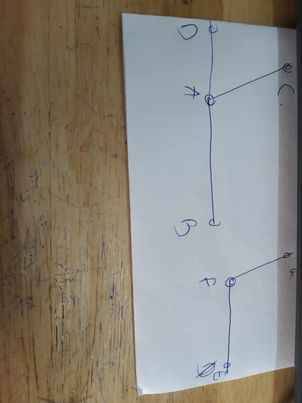
Ghi giả thiết, kết luận và chứng minh định lý: “ Hai góc cùng phụ với một góc thứ ba thì bằng nhau ”.
Chứng minh:
∠B phụ với ∠A ⇒ ∠B + ∠A = 90o ⇒ ∠B = 90o - ∠A
∠C phụ với ∠A ⇒ ∠C + ∠A = 90o ⇒ ∠C = 90o - ∠A
Vậy ∠B = ∠C.
Đúng 0
Bình luận (0)
vẽ hình và GHI GIẢ THIẾT,KẾT LUẬN VÀ CHỨNG MINH ĐỊNH LÍ:'' HAI GÓC CÙNG PHỤ VỚI MỘT GÓC THỨ BA THÌ BẰNG NHAU ''.
vẽ hình và GHI GIẢ THIẾT,KẾT LUẬN VÀ CHỨNG MINH ĐỊNH LÍ:'' HAI GÓC CÙNG PHỤ VỚI MỘT GÓC THỨ BA THÌ BẰNG NHAU ''.
Ta có : A1 + A2 = 90o
A3 + A2 = 90o
Mà A2 = A2
=> A1 = A3
Đúng 1
Bình luận (0)
Ta có: Góc xOy cộng góc yOz bằng 90 độ =>Góc xOy bằng 90 độ trừ số đo góc yOz
Góc zOt cộng góc yOz bằng 90 độ =>Góc zOt bằng 90 độ trừ số đo góc yOz
=>Góc xOy có số đo bằng góc zOt (cùng bằng 90 độ trừ số đo góc yOz)
Đúng 0
Bình luận (0)
ta co A2 +C = B+C (=90)
A2+C- C = B
=>A2=B
Đúng 0
Bình luận (0)
vẽ hình và GHI GIẢ THIẾT,KẾT LUẬN VÀ CHỨNG MINH ĐỊNH LÍ:'' HAI GÓC CÙNG PHỤ VỚI MỘT GÓC THỨ BA THÌ BẰNG NHAU ''
| Giả thiết | \(\widehat{mOy}+\widehat{yOn}=90^0;\widehat{xOn}+\widehat{yOn}=90^0\) |
| Két luận | \(\widehat{mOy}=\widehat{xOn}\) |
C/m
Ta có
\(\widehat{mOy}+\widehat{yOn}=90^0;\widehat{xOn}+\widehat{yOn}=90^0\)
\(\Rightarrow\widehat{mOy}+\widehat{yOn}=\widehat{xOn}+\widehat{yOn}\)
\(\Rightarrow\widehat{mOy}+\widehat{yOn}-\widehat{yOn}=\widehat{xOn}+\widehat{yOn}-\widehat{yOn}\)
\(\Rightarrow\widehat{mOy}=\widehat{xOn}\) (đpcm)
Đúng 0
Bình luận (2)
Hình tự vẽ nha!!!!
gt:hai góc cùng phụ
kl:hai góc bằng nhau
giai : goi hai góc a va b cùng phụ với c ta dược
a+c=90 =>a=90-c
b+c=90=>b=90-c
từ 2 điều trên suy ra a=b
Đúng 0
Bình luận (2)
vẽ hình hai góc cùng phụ với một góc thứ ba thì bằng nhau
vẽ hình hai góc cùng phụ vói một góc thứ ba thì bằng nhau
Đúng 0
Bình luận (0)
hai góc cùng bù với góc thứ ba thì bằng nhau
Đúng 0
Bình luận (0)
Chứng minh định lí: ''Hai góc cùng phụ với một góc thứ ba thì bằng nhau''.
Làm ơn ghi cách làm và vẽ hình.
Giả sử góc A và góc B cùng phụ với góc C => A + C = 900 , và B + C = 900.
=> A = 90 - C ; B = 90 - C
=> A = B
Đúng 0
Bình luận (0)
Vẽ hình minh họa, viết giả thiết- kết luận và chứng minh những định lý sau:
a,"hai góc đối đỉnh thì bằng nhau"
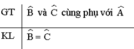
b,"hai đường thẳng phân biệt cùng vuông góc với một đường thảng thứ ba thì chúng song song với nhau"
giải giúp mình ạ mình cần gấp :<<
a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |
Đúng 0
Bình luận (0)