CMR a3 +b3+c3 chia hết cho 6 Nếu a+b+c chia hết cho 6 Với a, b, c thuộc Z
TN
Những câu hỏi liên quan
Cho các số nguyên a, b, c, d thỏa mãn a3+b3=5(c3+7d3). CMR a+b+c+d chia hết cho 6
cho a3+b3=2(c3-8d3); a,b,c,d ∈Z. CM a+b+c+d chia hết cho 3
Lời giải:
$a^3+b^3=2(c^3-8d^3)$
$a^3+b^3+c^3+d^3=c^3+d^3+2(c^3-8d^3)$
$=3c^3-15d^3=3(c^3-5d^3)\vdots 3$
Khi đó:
$(a+b+c+d)^3=(a+b)^3+(c+d)^3+3(a+b)(c+d)(a+b+c+d)$
$=a^3+b^3+c^3+d^3+3ab(a+b)+3cd(c+d)+3(a+b)(c+d)(a+b+c+d)\vdots 3$ do:
$a^3+b^3+c^3+d^3\vdots 3$
$3ab(a+b)\vdots 3$
$3cd(c+d)\vdots 3$
$3(a+b)(c+d)(a+b+c+d)\vdots 3$
Vậy:
$(a+b+c+d)^3\vdots 3$
$\Rightarrow a+b+c+d\vdots 3$
Đúng 4
Bình luận (4)
a) Chứng minh rằng: a3- a chia hết cho 6 với mọi giá trị a thuộc Z
b)Cho a,b,c thuộc Z thỏa mãn: a+b+c= 450 mũ 2023. Chứng minh rằng: a2+b2+c2 chia hết cho 6
a: a^3-a=a(a^2-1)
=a(a-1)(a+1)
Vì a;a-1;a+1 là ba số liên tiếp
nên a(a-1)(a+1) chia hết cho 3!=6
=>a^3-a chia hết cho 6
Đúng 0
Bình luận (0)
Cho 3 số nguyên dương a, b, c thỏa mãn a3 + b3 + c3 chia hết cho 14
CMR abc cũng chia hết cho 14
Rõ ràng trong hai số a, b, c tồn tại một số chẵn (Vì nếu a, b, c đều lẻ thì a3 + b3 + c3 là số lẻ, không chia hết cho 14).
Ta lại có \(a^3;b^3;c^3\equiv0;1;-1\).
Do đó nếu a, b, c đều không chia hết cho 7 thì \(a^3;b^3;c^3\equiv1;-1\left(mod7\right)\Rightarrow a^3+b^3+c^3⋮̸7\).
Đúng 0
Bình luận (0)
Làm tiếp: Suy ra trong ba số a, b, c có ít nhất một số chia hết cho 7 \(\Rightarrow abc⋮7\).
Vậy abc chia hết cho 14.
Đúng 0
Bình luận (0)
cho a,b,c,d thuộc z và (a+b+c+d) chia hết co 6
cmr : ( a mũ 3 + b mũ 3 + c mũ 3 + d mũ 3) chia hết cho 6
Bài này cần dùng một ít kiến thức của lớp 8, bạn có thể tìm hiểu thêm.
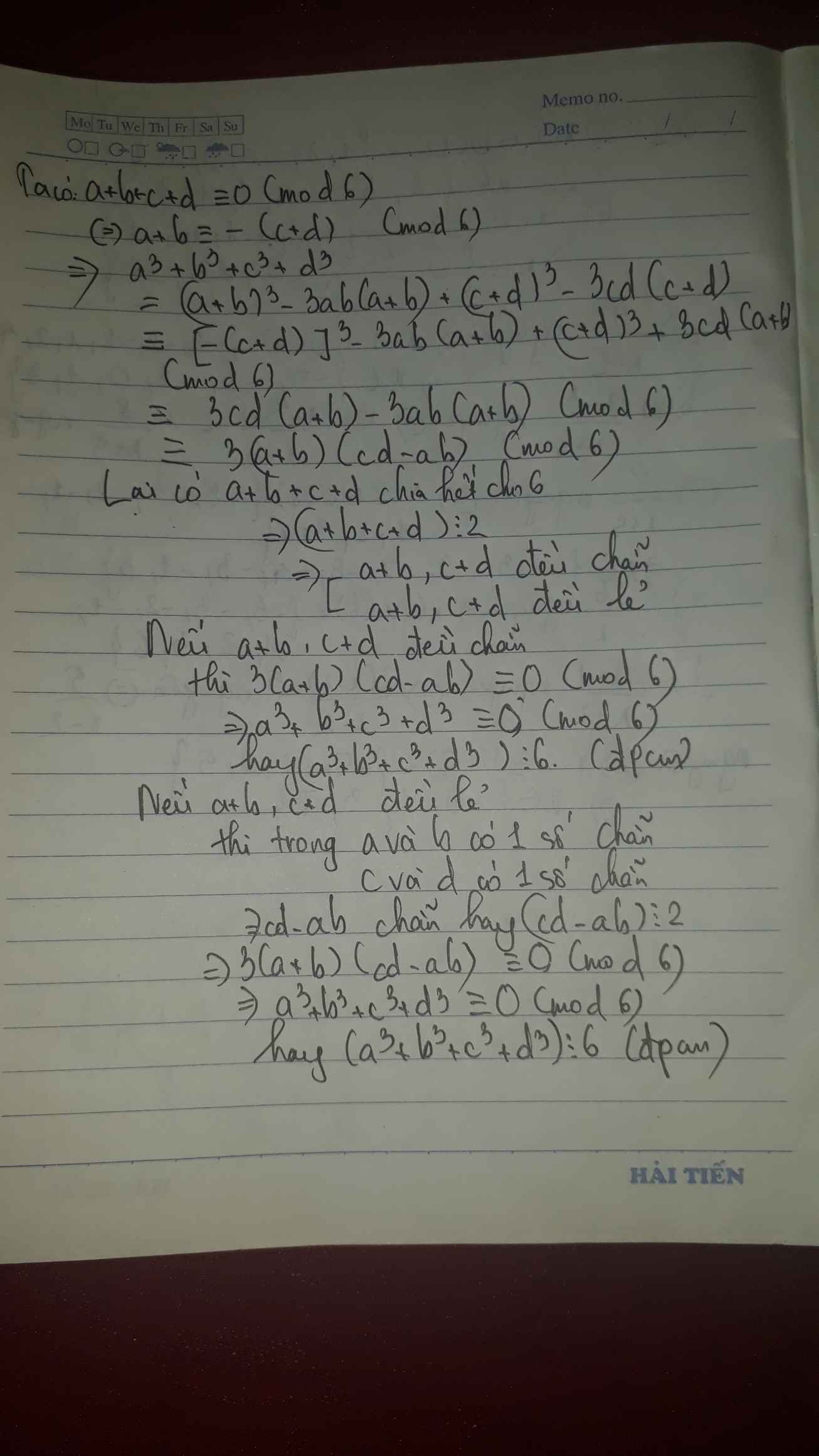
Đúng 1
Bình luận (0)
cho a,b,c,d thuộc z và (a+b+c+d) chia hết co 6
cmr : ( a mũ 3 + b mũ 3 + c mũ 3 + d mũ 3) chia hết cho 6
b1: cmr nếu x+y+z-3 thì (x+1)^3+(y+1)^3+(z+1)^3 3(x+1)(y+1)(z+1)b2: cho A+ (a^2+b^2-c^2)^2 -4a^2b^2 a) phân tích A thành nhân tử b) cm nếu a,b,c là số đo độ dài các cạnh của 1 tam giác thì A0b3: cho đa thức M(a+b)(b+c)(c+a)+abca/ phân tích M thành nhân tửb/ cm nếu a,b,c thuộc z và a+b+c chia hết cho 6 thì (M-3abc) chia hết cho 6b4: n thuộc z. cm n^3(n^2-7)^2 _ 36n chia hết cho 105b5: xác định a,b để đa thức x^4- 3x^3+3x^2+ ax+b chia hết cho đa thức x^2-3x+4.CÁC BẠN GIÚP MÌNH VỚI. CHIỀU P...
Đọc tiếp
b1: cmr nếu x+y+z=-3 thì (x+1)^3+(y+1)^3+(z+1)^3= 3(x+1)(y+1)(z+1)
b2: cho A+ (a^2+b^2-c^2)^2 -4a^2b^2
a) phân tích A thành nhân tử
b) cm nếu a,b,c là số đo độ dài các cạnh của 1 tam giác thì A<0
b3: cho đa thức M=(a+b)(b+c)(c+a)+abc
a/ phân tích M thành nhân tử
b/ cm nếu a,b,c thuộc z và a+b+c chia hết cho 6 thì (M-3abc) chia hết cho 6
b4: n thuộc z. cm n^3(n^2-7)^2 _ 36n chia hết cho 105
b5: xác định a,b để đa thức x^4- 3x^3+3x^2+ ax+b chia hết cho đa thức x^2-3x+4.
CÁC BẠN GIÚP MÌNH VỚI. CHIỀU PHẢI NỘP BÀI RỒI. HUHUHU :((((
Cho P = (a+b)(b+c)(c+a) - abc với a,b,c thuộc Z . Cmr nếu (a+c+b) chia hết cho 4 thì P chia hết cho 4
Ta có:P=(a+b)(a+c)(b+c)-abc=(a2b+ab2+b2c+bc2+a2c+ac2+abc+abc)-abc
=(a2b+ab2+abc)+(a2c+ac2+abc)+(b2c+bc2+abc)-2abc
=ab(a+b+c)+ac(a+b+c)+bc(a+b+c)-2abc
=(a+b+c)(ab+ac+bc)-2abc
thấy a+b+c chia hết cho 4 => (a+b+c)(ab+bc+ac) chia hết cho 4 (1)
Do a+b+c chia hết cho 4 => tồn tại ít nhất trong 3 số a,b,c một số chia hết cho 2=>2abc chia hết cho 4 (2)
Tù (1) và (2)=>P chia hết cho 4
Đúng 0
Bình luận (0)
cho a,b,c thuộc Z . CMR A=(a-b).(b-c).(c-a) chia hết cho 6 biết rằng không tồn tại số nào chia hết cho 3



