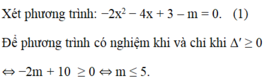tìm tất cả các giá trị thực của m để phương trình 4x^2-2x^2+2+6=m
NN
Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để phương trình
4
x
−
2
m
.2
x
+
m
+
2
0
có 2 nghiệm phân biệt. A.
−
2
m
2
B.
m
−
2
C. m 2 D. m 2
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 4 x − 2 m .2 x + m + 2 = 0 có 2 nghiệm phân biệt.
A. − 2 < m < 2
B. m > − 2
C. m > 2
D. m < 2
Đáp án C
Phương pháp:
Đặt 2 x = t t > 0 , đưa về phương trình bậc 2 ẩn t, tìm điều kiện của phương trình bậc 2 ẩn t để phương trình ban đầu có 2 nghiệm phân biệt.
Cách giải: Đặt 2 x = t t > 0 khi đó phương trình trở thành t 2 − 2 m t + m + 2 = 0 *
Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.
Khi đó: Δ ' > 0 S > 0 P > 0 ⇔ m 2 − m − 2 > 0 2 m > 0 m + 2 > 0 ⇔ m > 2 m < − 1 m > 0 m > − 2 ⇒ m > 2
Chú ý và sai lầm: Rất nhiều học sinh sau khi đặt ẩn phụ thì quên mất điều kiện t > 0, dẫn đến việc chỉ đi tìm điều kiện đề phương trình (*) có 2 nghiệm phân biệt.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
9
.
9
x
2
-
2
x
–
(
2
m
+
1
)
15
x
2
-
2
x
+
1
+...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 9 . 9 x 2 - 2 x – ( 2 m + 1 ) 15 x 2 - 2 x + 1 + 4 m - 2 5 2 x 2 - 4 x + 2 = 0 có 2 nghiệm thực phân biệt
A. 1 2 < m < 1
B. m > 3 + 6 2 hoặc m < 3 - 6 2
C. m > 1 hoặc m < 1 2
D. 3 - 6 2 < m < 3 + 6 2
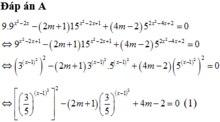

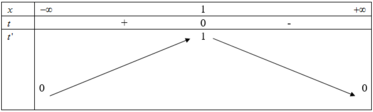
Dựa vào bảng biến thiên hàm f(x), ta thấy để phương trình (1) có 2 nghiệm thực x phân biệt thì phương trình (2) phải có duy nhất 1 nghiệm thuộc khoảng (0;1), nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao điểm của đồ thị hàm số y = 3 5 x - 1 2 và đường thẳng y = 2 m - 1 nên điều kiện của m thỏa mãn là 0 < 2 m - 1 < 1 ⇔ 1 2 < m < 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của m để phương trình −2 x 2 − 4x + 3 = m có nghiệm.
A. 1 ≤ m ≤ 5.
B. −4 ≤ m ≤ 0.
C. 0 ≤ m ≤ 4.
D. m ≤ 5.
ĐỀ THI HỌC KỲ I Câu 1 : giải phương trình ln (3x2 - 2x +1) ln ( 4x - 1) Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 m sqrt{9^x+1} có đúng 1 nghiệm Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Đọc tiếp
ĐỀ THI HỌC KỲ I
Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1)
Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm
Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Tìm tất cả các giá trị của tham số m để phương trình 4x+1- 2x+2 + m = 0 có nghiệm.
A. m ≤ 0
B. m ≥ 0
C. m ≤ 1
D. m ≥ 1
Tìm tất cả các giá trị thực của tham số m để bất phương trình
4
x
-
m
.
2
x
+
1
+
3
-
2
m
≤
0
có nghiệm thực A.
m
≥
2
B.
m
≤
3
C.
m
≤
5
D.
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 4 x - m . 2 x + 1 + 3 - 2 m ≤ 0 có nghiệm thực
A. m ≥ 2
B. m ≤ 3
C. m ≤ 5
D. m ≥ 1
Đáp án D

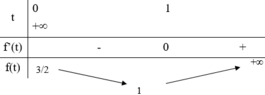
Vậy để bất phương trình có nghiệm thực thì m ≥ 1
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
2
x
-
1
x
+
2
m
có 2 nghiệm phân biệt. A.
m
∈
1
;
5
2
B.
m
∈...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 x - 1 x + 2 = m có 2 nghiệm phân biệt.
A. m ∈ 1 ; 5 2
B. m ∈ - 2 ; 1 2
C. m ∈ 0 ; 3
D. m ∈ - 1 2 ; 2
Chọn đáp án D

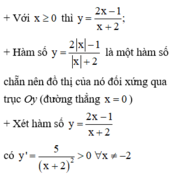
nên là hàm đồng biến trên từng khoảng xác định.
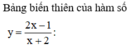
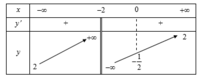
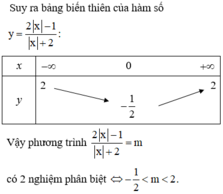

Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
m
.
4
x
+
(
m
-
1
)
2
x
+
2
+
m
-
1
0
nghiệm đúng
∀
x
∈
ℝ
? A.
m
≤
3
. B.
m
≥...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình m . 4 x + ( m - 1 ) 2 x + 2 + m - 1 > 0 nghiệm đúng ∀ x ∈ ℝ ?
A. m ≤ 3 .
B. m ≥ 1 .
C. - 1 ≤ m ≤ 4 .
D. m ≥ 0 .
tìm tất cả các giá trị thực của tham số m để phương trình \(^{x^2-2x+\sqrt{-x^2+2x}-3+m=0}\) có nghiệm
Đặt \(-x^2+2x=t\Rightarrow0\le t\le1\)
\(\Rightarrow-t^2+t-3+m=0\)
\(\Leftrightarrow t^2-t+3=m\)
Xét hàm \(f\left(t\right)=t^2-t+3\) trên \(\left[0;1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[0;1\right]\)
\(f\left(0\right)=3\) ; \(f\left(1\right)=3\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{11}{4}\)
\(\Rightarrow\dfrac{11}{4}\le f\left(t\right)\le3\)
\(\Rightarrow\) Pt có nghiệm khi và chỉ khi \(\dfrac{11}{4}\le m\le3\)
Đúng 0
Bình luận (0)
Cho phương trình
4
x
2
-
2
x
+
1
-
m
.
2
x
2
-
2
x
+
2
+
3
m
-
2
0...
Đọc tiếp
Cho phương trình 4 x 2 - 2 x + 1 - m . 2 x 2 - 2 x + 2 + 3 m - 2 = 0 với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có bốn nghiệm phân biệt.
A. m < 1
B. m < 1; m > 2
C. m ≥ 2
D. m > 2