a) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOc}< \widehat{aOb}\left(50^0< 120^0\right)\)

nên tia Oc nằm giữa hai tia Oa và Ob

\(\Leftrightarrow\widehat{aOc}+\widehat{bOc}=\widehat{aOb}\)

\(\Leftrightarrow\widehat{bOc}=\widehat{aOb}-\widehat{aOc}=120^0-50^0=70^0\)

Ta có: Om là tia phân giác của \(\widehat{bOc}\)(gt)

nên \(\widehat{bOm}=\dfrac{\widehat{bOc}}{2}=\dfrac{70^0}{2}\)

hay \(\widehat{bOm}=35^0\)

Vậy: \(\widehat{bOm}=35^0\)

có muốn giải giúp ko

a) Các góc kề với \(\widehat {tOz}\)là: \(\widehat {zOy},\widehat {zOn},\widehat {zOm}\)

b) Ta có: \(\widehat {mOn}\) = 30\(^\circ \) nên góc kề bù với \(\widehat {mOn}\) có số đo là: 180\(^\circ \) - 30\(^\circ \) = 150\(^\circ \)

c) Ta có:

\(\begin{array}{l}\widehat {mOn} + \widehat {nOy} + \widehat {yOt} = 180^\circ \\ \Rightarrow 30^\circ  + \widehat {nOy} + 90^\circ  = 180^\circ \\ \Rightarrow \widehat {nOy} = 180^\circ  - 30^\circ  - 90^\circ  = 60^\circ \end{array}\)

Vậy \(\widehat {nOy} = 60^\circ \)

d) Ta có: \(\widehat {tOz} = 45^\circ \) nên góc kề bù với \(\widehat {tOz}\) có số đo là: 180\(^\circ \) - 45\(^\circ \) = 135\(^\circ \)

Sửa đề: A'OC đối đỉnh với AOB

góc A'OC=góc AOB=40 độ

góc AOC=180-40=140 độ

góc AOM=góc MOC=140/2=70 độ

câu a mọi người ko cần vẽ hình nữa nha

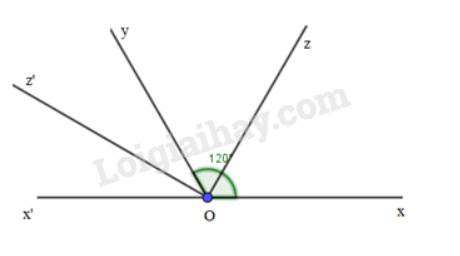
Vì Oz là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOz} = \widehat {zOy} = \frac{1}{2}.\widehat {xOy} = \frac{1}{2}.120^\circ  = 60^\circ \)

Vì Oz’ là tia phân giác của \(\widehat {yOx'}\) nên \(\widehat {x'Oz'} = \widehat {yOz'} = \frac{1}{2}.\widehat {yOx'} = \frac{1}{2}.60^\circ  = 30^\circ \)

Vì tia Oy nằm trong \(\widehat {zOz'}\) nên \(\widehat {zOz'}=\widehat {zOy} + \widehat {yOz'} =  60^\circ  + 30^\circ  = 90^\circ \)

Vậy \(\widehat {zOy} = 60^\circ ,\widehat {yOz'} = 30^\circ ,\widehat {zOz'} = 90^\circ \)

Chú ý:

2 tia phân giác của 2 góc kề bù thì vuông góc với nhau

a) Ta có \(\widehat{xOy}\) và \(\widehat{yOz}\) là 2 góc kề bù (theo đề)
   \(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
   Hay \(50^0+\widehat{yOz}=180^0\)
                   \(\Rightarrow\widehat{yOz}=130^0\)

b) Góc mOn ..... bn tự lm ik
 Ta có: Om là tia phân giác của \(\widehat{xOy}\) (theo đề)
 \(\Rightarrow\)\(\widehat{xOm}=\widehat{yOm}=\frac{\widehat{xOy}}{2}=\frac{50^0}{2}=25^0\)
Lại có : On là tia phân giác của \(\widehat{yOz}\) (theo đề)
\(\Rightarrow\)\(\widehat{yOn}=\widehat{zOn}=\frac{\widehat{yOz}}{2}=\frac{130^0}{2}=65^0\)
Ta lại có: \(\widehat{mOy} + \widehat{nOy} = 25^0 + 65^0 = 90^0\)
 Do đó 2 góc mOy và nOy phụ nhau.