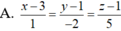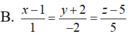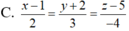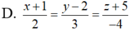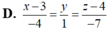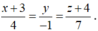Cho hai điểm A(1;-2;3), B(-1;4;1) và đường thẳng d : x + 2 1 = y - 2 - 1 = z + 3 2 . Phương trình nào sau đây là phương trình đường thẳng đi qua trung điểm của đoạn thẳng AB và song song với d?
A. x 1 = y - 1 - 1 = z + 1 2
B. x 1 = y - 1 1 = z + 1 2
C. x 1 = y - 1 - 1 = z + 2 2
D. x - 1 1 = y - 1 - 1 = z + 1 2