biết x2+y2=4x+6y+6. Giá trị lớn nhất của 3x+4y là gì
TT
Những câu hỏi liên quan
Cho hai số thực x, y thỏa mãn
x
2
+
y
2
-
4
x
+
6
y
+
4
+
y
2
+
6
y
+
10
6
+
4
x
-
x
2...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 + y 2 - 4 x + 6 y + 4 + y 2 + 6 y + 10 = 6 + 4 x - x 2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T = x 2 + y 2 - a . Có bao nhiêu giá trị nguyên thuộc đoạn [-10;10] của tham số a để M ≥ 2 m
A. 17
B. 16
C. 15
D. 18
Chọn B.
Phương pháp:
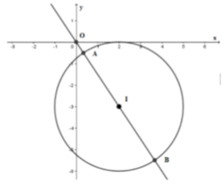
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
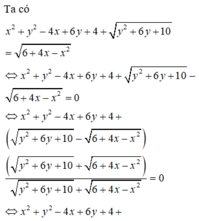
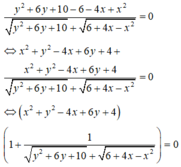


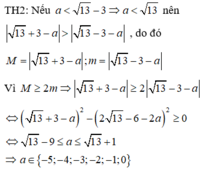

Đúng 0
Bình luận (0)
Xét các số thực x, y thỏa mãn
x
2
+
y
2
≥
4
và
l
o
g
x
2
+
y
2
(
4
x
-
2
y
)
≥
1
. Giá trị lớn nhất của biểu thức P3x+4y-5 là với a, b là các số nguyên. Tính
T
a
3...
Đọc tiếp
Xét các số thực x, y thỏa mãn x 2 + y 2 ≥ 4 và l o g x 2 + y 2 ( 4 x - 2 y ) ≥ 1 . Giá trị lớn nhất của biểu thức P=3x+4y-5 là với a, b là các số nguyên. Tính T = a 3 + b 3
A. 0
B. 250
C. 152
D. 98
tìm giá trị lớn nhất của biểu thức : P=-x2-y2+4x-4y+2
\(P=-x^2-y^2+4x-4y+2=-\left(x^2-4x+4\right)-\left(y^2+4y+4\right)+10=-\left(x-2\right)^2-\left(y+2\right)^2+10\le10\)
Dấu = xảy ra khi x = 2; y = -2
Đúng 1
Bình luận (0)
Cho đường tròn (C): x 2 + y 2 + 8 x + 6 y + 5 = 0 và đường thẳng ∆: 3x – 4y + m = 0. Giá trị của m để đường thẳng cắt đường tròn theo dây cung dài nhất là
A. m = 0
B. m = 2
C. m = 4
D. m = 6
Đường tròn đã cho có tâm I( - 4; -3).
Để đường thẳng ∆ cắt đường tròn theo dây cung dài nhất thì điểm I nằm trên ∆.
Suy ra: 3. (-4) – 4. (-3) + m = 0
⇔ − 12 + 12 + m = 0 ⇔ m = 0
Đáp án A
Đúng 0
Bình luận (0)
Bài 6:Tìm giá trị lớn nhất của biểu thứca) A-x2+6x-11 b) B5-8x-x2 c) C4x-x2+1Bài 7:Tìm giá trị nhỏ nhất của biểu thứca) Ax2-6x+11 b) Bx2-2x+y2+4y+8 c) Cx2-4xy+5y2+10x-22y+28
Đọc tiếp
Bài 6:Tìm giá trị lớn nhất của biểu thức
a) A=-x2+6x-11 b) B=5-8x-x2 c) C=4x-x2+1
Bài 7:Tìm giá trị nhỏ nhất của biểu thức
a) A=x2-6x+11 b) B=x2-2x+y2+4y+8 c) C=x2-4xy+5y2+10x-22y+28
Bài 6:
a) Ta có: \(A=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu '=' xảy ra khi x=3
b) Ta có: \(B=-x^2-8x+5\)
\(=-\left(x^2+8x-5\right)\)
\(=-\left(x^2+8x+16-21\right)\)
\(=-\left(x+4\right)^2+21\le21\forall x\)
Dấu '=' xảy ra khi x=-4
c) Ta có: \(C=-x^2+4x+1\)
\(=-\left(x^2-4x-1\right)\)
\(=-\left(x^2-4x+4-5\right)\)
\(=-\left(x-2\right)^2+5\le5\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
Bài 7:
a) Ta có: \(x^2-6x+11\)
\(=x^2-6x+9+2\)
\(=\left(x-3\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=3
Đúng 0
Bình luận (0)
Phương trình nào sau đây là phương trình của đường tròn? (I) x2+ y2 – 4x +15y -12 0. (II) x2+ y2 – 3x +4y +20 0. (III) 2x2+ 2y2- 4x + 6y +1 0 . A. Chỉ (I). B. Chỉ (II). C. Chỉ (III). D. Chỉ (I) và (III).
Đọc tiếp
Phương trình nào sau đây là phương trình của đường tròn?
(I) x2+ y2 – 4x +15y -12= 0.
(II) x2+ y2 – 3x +4y +20= 0.
(III) 2x2+ 2y2- 4x + 6y +1= 0 .
A. Chỉ (I).
B. Chỉ (II).
C. Chỉ (III).
D. Chỉ (I) và (III).
Ta xét các phương án:
(I) có:
![]()
(II) có:
![]()
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
![]()
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất
A= 15-8x-x2
B=4x-x2+2
C= x2 - y2+4x+4y+2
\(A=15-8x-x^2=-\left(x+4\right)^2+31\)
Vì \(\left(x+4\right)^2\ge0\forall x\)\(\Rightarrow-\left(x+4\right)^2+31\le31\)
Dấu "=" xảy ra \(\Leftrightarrow-\left(x+4\right)^2=0\Leftrightarrow x=-4\)
Vậy maxA = 31 <=> x = - 4
\(B=4x-x^2+2=-\left(x-2\right)^2+6\)
Vì \(\left(x-2\right)^2\ge0\forall x\)\(\Rightarrow-\left(x-2\right)^2+6\le6\)
Dấu "=" xảy ra \(\Leftrightarrow-\left(x-2\right)^2=0\Leftrightarrow x=2\)
Vậy maxB = 6 <=> x = 2
a) \(A=15-8x-x^2=-\left(x^2+8x+16\right)-1\)
\(=-\left(x+4\right)^2-1\le-1\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(-\left(x+4\right)=0\Rightarrow x=-4\)
b) \(B=4x-x^2+2=-\left(x^2-4x+4\right)+6\)
\(=-\left(x-2\right)^2+6\le6\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(-\left(x-2\right)^2=0\Rightarrow x=2\)
c) Trang nghĩ nên sửa đề nhé:
\(C=-x^2-y^2+4x+4y+2\)
\(C=-\left(x^2-4x+4\right)-\left(y^2-4y+4\right)+10\)
\(C=-\left(x-2\right)^2-\left(y-2\right)^2+10\le10\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}-\left(x-2\right)^2=0\\-\left(y-2\right)^2=0\end{cases}}\Rightarrow x=y=2\)
A = 15 - 8x - x2
= -( x2 + 8x + 16 ) + 31
= -( x + 4 )2 + 31
-( x + 4 )2 ≤ 0 ∀ x => -( x + 4 )2 + 31 ≤ 31
Đẳng thức xảy ra <=> x + 4 = 0 => x = -4
=> MaxA = 31 <=> x = -4
B = 4x - x2 + 2
= -( x2 - 4x + 4 ) + 6
= -( x - 2 )2 + 6
-( x - 2 )2 ≤ 0 ∀ x => -( x - 2 )2 + 6 ≤ 6
Đẳng thức xảy ra <=> x - 2 = 0 => x = 2
=> MaxB = 6 <=> x = 2
C = -x2 - y2 + 4x + 4y + 2 ( -x2 mới ra :v )
= -( x2 - 4x + 4 ) - ( y2 - 4y + 4 ) + 10
= -( x - 2 )2 - ( y - 2 )2 + 10
\(\hept{\begin{cases}-\left(x-2\right)^2\le0\forall x\\-\left(y-2\right)^2\le0\forall y\end{cases}}\Rightarrow-\left(x-2\right)^2-\left(y-2\right)^2+10\le10\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-2=0\\y-2=0\end{cases}}\Leftrightarrow x=y=2\)
=> MaxC = 10 <=> x = y = 2
Xem thêm câu trả lời
Tìm giá trị nhỏ nhất của biểu thức:
a, 3x2 – 3x + 1
b, x2 – 2x + y2 + 4y + 6
c, 2x2 + y2 – 2xy + 1
\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)
Đúng 0
Bình luận (0)
Bài 1: Tìm giá trị nhỏ nhất của:a) A x2 + 2x + 4b) B x2 - 20x + 101c) C x2 - 2x + y2 + 4y + 8 Bài 2: Tìm giá trị lớn nhất của:A 5 - 8x - x2B x - x2C 4x - x2 + 3D -x2 + 6x - 11
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất của:
a) A= x2 + 2x + 4
b) B= x2 - 20x + 101
c) C= x2 - 2x + y2 + 4y + 8
Bài 2: Tìm giá trị lớn nhất của:
A = 5 - 8x - x2
B = x - x2
C = 4x - x2 + 3
D = -x2 + 6x - 11
Bài 1:
a: \(A=x^2+2x+4\)
\(=x^2+2x+1+3\)
\(=\left(x+1\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x+1=0
=>x=-1
Vậy: \(A_{min}=3\) khi x=-1
b: \(B=x^2-20x+101\)
\(=x^2-20x+100+1\)
\(=\left(x-10\right)^2+1>=1\forall x\)
Dấu '=' xảy ra khi x-10=0
=>x=10
Vậy: \(B_{min}=1\) khi x=10
c: \(C=x^2-2x+y^2+4y+8\)
\(=x^2-2x+1+y^2+4y+4+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x-1=0 và y+2=0
=>x=1 và y=-2
Vậy: \(C_{min}=3\) khi (x,y)=(1;-2)
Bài 2:
a: \(A=5-8x-x^2\)
\(=-\left(x^2+8x\right)+5\)
\(=-\left(x^2+8x+16-16\right)+5\)
\(=-\left(x+4\right)^2+16+5=-\left(x+4\right)^2+21< =21\forall x\)
Dấu '=' xảy ra khi x+4=0
=>x=-4
b: \(B=x-x^2\)
\(=-\left(x^2-x\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
c: \(C=4x-x^2+3\)
\(=-x^2+4x-4+7\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
d: \(D=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x^2-6x+9+2\right)\)
\(=-\left(x-3\right)^2-2< =-2\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
Đúng 4
Bình luận (0)







