Cho x + 2y + 3z= 5. Tìm GTNN của Q= x2 + y2 + z2
CN
Những câu hỏi liên quan
Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 3z + 1 0 và mặt cầu (S):
x
2
+
y
2
+
z
2
- 2x - 4y + 6z + 5 0. Khẳng định nào dưới đây là đúng? A. (P) giao (S) theo một đường tròn B. (P) tiếp xúc với (S) C. (P) không cắt (S) D. Cả ba khẳng định trên đều sai
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 3z + 1 = 0 và mặt cầu (S): x 2 + y 2 + z 2 - 2x - 4y + 6z + 5 = 0. Khẳng định nào dưới đây là đúng?
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Cả ba khẳng định trên đều sai
Đáp án A
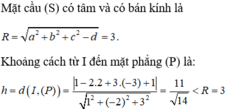
Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 - 2x - 4y + 6z + 5 0 và cho mặt phẳng (P) : x - 2y + 3z + 3 0. Khẳng định nào dưới đây là đúng ? A. (P) giao (S) theo một đường tròn B. (P) tiếp xúc với (S) C. (P) không cắt (S) D. Mặt phẳng (P) đi qua tâm của mặt cầu (S)
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 - 2x - 4y + 6z + 5 = 0 và cho mặt phẳng (P) : x - 2y + 3z + 3 = 0. Khẳng định nào dưới đây là đúng ?
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Mặt phẳng (P) đi qua tâm của mặt cầu (S)
Đáp án A
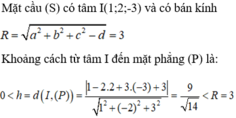
Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn và (P) không đi qua tâm I của (S).
Vậy đáp án đúng là A.
Đúng 0
Bình luận (0)
Cho các số x,y,z dương thỏa mãn:
x2 +y2 +z2 = 1. Tìm GTNN của M= 1/16x2 +1/4y2 + 1/z2
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{49}{16}\)
\(M_{min}=\dfrac{49}{16}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{\sqrt{7}};\dfrac{2}{\sqrt{14}};\dfrac{2}{\sqrt{7}}\right)\)
Đúng 1
Bình luận (1)
Cho các số x,y,z dương thỏa mãn:
x2 +y2 +z2 = 7/4. Tìm GTNN của M= 1/16x2 +1/4y2 + 1/z2
\(M=\dfrac{\dfrac{1}{16}}{x^2}+\dfrac{\dfrac{1}{4}}{y^2}+\dfrac{1}{z^2}\ge\dfrac{\left(\dfrac{1}{4}+\dfrac{1}{2}+1\right)^2}{x^2+y^2+z^2}=\dfrac{7}{4}\)
\(M_{min}=\dfrac{7}{4}\) khi \(\left(x;y;z\right)=\left(\dfrac{1}{2};\dfrac{1}{\sqrt{2}};1\right)\)
Đúng 3
Bình luận (2)
cho x+y+z=4 xy+xz+xt+yz+yt+zt=1 tìm GTNN của x2+y2+z2+t2
Cho x + y + z = 3
a, Tìm GTNN của A = x2 + y2 + z2
b, Tìm GTNN của B = xy + yz + zx
c, Tìm GTNN của C = A + B
a, ap dung bunhiacopxki
(1+1+1)A\(\ge\)(x+y+z)2=9
A\(\ge\)3
Dau bang xay ra khi x=y=z=1
b, co Bmax ko co Bmin
Đúng 0
Bình luận (0)
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
Vị trí tương đối của hai mặt cầu:
x
2
+
y
2
+
z
2
+ 2x - 2y - 2z - 7 0 và
x
2
+
y
2
+
z
2
+ 2x + 2y + 4z + 5 0 là: A. ở ngoài nhau B. tiếp xúc C. cắt nhau D....
Đọc tiếp
Vị trí tương đối của hai mặt cầu: x 2 + y 2 + z 2 + 2x - 2y - 2z - 7 = 0 và x 2 + y 2 + z 2 + 2x + 2y + 4z + 5 = 0 là:
A. ở ngoài nhau
B. tiếp xúc
C. cắt nhau
D. chứa nhau
Đáp án C
Mặt cầu: x 2 + y 2 + z 2 + 2x - 2y – 2z – 7 = 0 có tâm I(-1; 1;1) và
Mặt cầu: x 2 + y 2 + z 2 + 2x + 2y + 4z + 5= 0 có tâm I’( -1; -1; -2) và R’ = 1
![]()
Do đó, hai mặt cầu này cắt nhau.
Đúng 0
Bình luận (0)
cho x, y, z ≥ 0 thỏa mãn x + y + z =6. Tìm GTNN và GTLN của
A = x2 + y2 + z2
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
Đúng 0
Bình luận (0)
Tìm x, y, z biết: 5x = 7y = 3z và x2 + y2 - z2 = 585
Ta has: x2+y2≥2xyx ^ 2 + y ^ 2 \ ge2xyx2+y2≥2 x y
⇔2(x2+y2)≥(x+y)2\ Leftrightarrow2 \ left (x ^ 2 + y ^ 2 \ right) \ ge \ left (x + y \ right) ^ 2⇔2( x2+y2)≥( x+y )2
⇔x2+y2≥(x+y)22\ Leftrightarrow x ^ 2 + y ^ 2 \ ge \ frac {\ left (x + y \ right) ^ 2} {2}⇔x2+y2≥2( x + y )2Các bác sĩ cho biết thêm:
Áp dụng vào bài toán có:
P≤x+y(x+y)22+y+z(y+z)22+z+x(z+x)22P \ le \ frac {x + y} {\ frac {\ left (x + y \ right) ^ 2} {2}} + \ frac {y + z} {\ frac {\ left (y + z \ right ) ^ 2} {2}} + \ frac {z + x} {\ frac {\ left (z + x \ right) ^ 2} {2}}P≤2( x + y )2Các bác sĩ cho biết thêm:x + yCác bác sĩ cho biết thêm:+2( y + z )2Các bác sĩ cho biết thêm:y + zCác bác sĩ cho biết thêm:+2( z + x )2Các bác sĩ cho biết thêm:z + xCác bác sĩ cho biết thêm: =2x+y+2y+z+2z+x=12(4x+y+4y+z+4z+x)= \ frac {2} {x + y} + \ frac {2} {y + z} + \ frac {2} {z + x} = \ frac {1} {2} \ left (\ frac {4} {x + y} + \ frac {4} {y + z} + \ frac {4} {z + x} \ right)=x + y2Các bác sĩ cho biết thêm:+y + z2Các bác sĩ cho biết thêm:+z + x2Các bác sĩ cho biết thêm:=21Các bác sĩ cho biết thêm:(x + y4Các bác sĩ cho biết thêm:+y + z4Các bác sĩ cho biết thêm:+z + x4Các bác sĩ cho biết thêm:)
Áp dụng BĐT Svacxo ta có:
4x+y≤1x+1y\ frac {4} {x + y} \ le \ frac {1} {x} + \ frac {1} {y}x + y4Các bác sĩ cho biết thêm:≤x1Các bác sĩ cho biết thêm:+y1Các bác sĩ cho biết thêm:, 4y+z≤1y+1z\ frac {4} {y + z} \ le \ frac {1} {y} + \ frac {1} {z}y + z4Các bác sĩ cho biết thêm:≤y1Các bác sĩ cho biết thêm:+z1Các bác sĩ cho biết thêm:, 4z+x≤1z+1x\ frac {4} {z + x} \ le \ frac {1} {z} + \ frac {1} {x}z + x4Các bác sĩ cho biết thêm:≤z1Các bác sĩ cho biết thêm:+x1Các bác sĩ cho biết thêm:
Do đó: P≤12[2.(1x+1y+1z)]=2016P \ le \ frac {1} {2} \ left [2. \ left (\ frac {1} {x} + \ frac {1} {y} + \ frac {1} {z} \ right) \ right ] = 2016P≤21Các bác sĩ cho biết thêm:[ 2 .(x1Các bác sĩ cho biết thêm:+y1Các bác sĩ cho biết thêm:+z1Các bác sĩ cho biết thêm:) ]=2 0 1 6
Dấu "=" ⇔x=y=z=1672\ Leftrightarrow x = y = z = \ frac {1} {672}⇔x=y=z=6 7 21Các bác sĩ cho biết thêm:
P / s: Dấu "=" không chắc lắm :))
Học tốt đêý nhá
ta có 5x=7y=3z= \(\frac{x}{5}=\frac{y}{7}=\frac{z}{3}\)=> \(\frac{x^2}{25}=\frac{y^2}{49}=\frac{z^2}{9}\)
ADTC dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{25}=\frac{y^2}{49}=\frac{z^2}{9}=\frac{x^2+y^2-z^2}{25+49-9}=\frac{585}{65}=9\)
Suy ra:
\(\frac{x^2}{25}=9\Rightarrow x^2=25.9\Rightarrow x^2=225\Rightarrow x^2=15^2\Rightarrow x=15\)
\(\frac{y^2}{49}=9\Rightarrow y^2=9.49\Rightarrow y^2=441\Rightarrow y^2=21^2\Rightarrow y=21\)
\(\frac{z^2}{9}=9\Rightarrow z^2=9.9\Rightarrow z^2=81\Rightarrow z^2=9^2\Rightarrow z=9\)
Vậy x = 15;y=21;z=9

