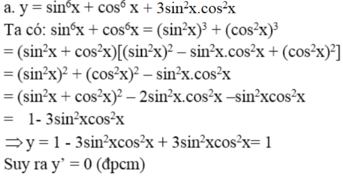a: \(=\left(\sin^2\alpha+\cos^2\alpha\right)^2=1^2=1\)

Chứng minh các biểu thức đã cho không phụ thuộc vào x.

f(x) = 1 ⇒ f′(x) = 0

\(A=3\left[\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\right]-2\left[\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\right]\)
 

\(=3\left[1-2\cdot sin^2x\cdot cos^2x\right]-2\left[1-3\cdot sin^2x\cdot cos^2x\right]\)

\(=3-6\cdot sin^2x\cdot cos^2x-2+6\cdot sin^2x\cdot cos^2x\)

=1

a, Ta có:  sin 4 x + cos 4 x = sin 2 x + cos 2 x 2 - 2 sin 2 x . cos 2 x = 1 - 2 sin 2 x . cos 2 x

b, Ta có:  sin 6 x + cos 6 x = sin 2 x + cos 2 x 3 - 3 sin 2 x cos 2 x sin 2 x + cos 2 x =  1 - 3 sin 2 x cos 2 x

1.

\(y=\sqrt{5-2\cos ^2x\sin ^2x}=\sqrt{5-\frac{1}{2}(2\cos x\sin x)^2}=\sqrt{5-\frac{1}{2}\sin ^22x}\)

Dễ thấy:

$\sin ^22x\geq 0\Rightarrow y=\sqrt{5-\frac{1}{2}\sin ^22x}\leq \sqrt{5}$

Vậy $y_{\max}=\sqrt{5}$

$\sin ^22x\leq 1\Rightarrow y=\sqrt{5-\frac{1}{2}\sin ^22x}\geq \sqrt{5-\frac{1}{2}}=\frac{3\sqrt{2}}{2}$

Vậy $y_{\min}=\frac{3\sqrt{2}}{2}$

2.

$y=1+\frac{1}{2}\sin 2x\cos 2x=1+\frac{1}{4}.2\sin 2x\cos 2x$

$=1+\frac{1}{4}\sin 4x$

Vì $-1\leq \sin 4x\leq 1$

$\Rightarrow \frac{5}{4}\leq 1+\frac{1}{4}\sin 4x\leq \frac{3}{4}$

$\Leftrightarrow \frac{5}{4}\leq y\leq \frac{3}{4}$
Vậy $y_{\max}=\frac{5}{4}; y_{\min}=\frac{3}{4}$

3.

$\sin x\geq -1\Rightarrow \sqrt{1+\sin x}\geq 0$

$\Rightarrow y\geq -3$

Vậy $y_{\min}=-3$

$\sin x\leq 1\Rightarrow \sqrt{1+\sin x}\leq \sqrt{2}$

$\Rightarrow y\leq \sqrt{2}-3$
Vậy $y_{\max}=\sqrt{2}-3$

Câu a)

Đặt \(2x=a\). PT trở thành:

\(2\sin ^2a+\sin 3a-1=\sin a\)

\(\Leftrightarrow 2\sin ^2a+\sin (a+2a)-1-\sin a=0\)

\(\Leftrightarrow 2\sin ^2a+\sin a\cos 2a+\cos a\sin 2a-1-\sin a=0\)

\(\Leftrightarrow 2\sin ^2a+\sin a\cos 2a+2\cos ^2a\sin a-1-\sin a=0\)

\(\Leftrightarrow (2\sin ^2a-1)+\sin a\cos 2a+\sin a(2\cos ^2a-1)=0\)

\(\Leftrightarrow -\cos 2a+\sin a\cos 2a+\sin a\cos 2a=0\)

\(\Leftrightarrow \cos 2a(-1+2\sin a)=0\)

\(\Rightarrow \left[\begin{matrix} \cos 2a=0(1)\\ \sin a=\frac{1}{2}(2)\end{matrix}\right.\)

Từ (1) \(\Rightarrow 2a=\frac{\pi}{2}+k\pi (k\in\mathbb{Z})\)\(\Rightarrow x=\frac{\pi}{8}+\frac{k\pi}{4}\)

Từ (2) \(\Rightarrow \left[\begin{matrix} a=\frac{\pi}{6}+2k\pi \rightarrow x=\frac{\pi}{12}+k\pi \\ a=\frac{5}{6}\pi+2k\pi \rightarrow x=\frac{5\pi}{12}+k\pi \end{matrix}\right.\)

Bài 2:

\(\sin 2x+\sin 6x+2\sin ^2x-1=0\)

\(\Leftrightarrow \sin 2x+\sin 6x-\cos 2x=0\)

\(\Leftrightarrow \sin 2x+\sin 4x\cos 2x+\cos 4x\sin 2x-\cos 2x=0\)

\(\Leftrightarrow \sin a+\sin 2a\cos a+\cos 2a\sin a-\cos a=0\)

\(\Leftrightarrow \sin a(1+\cos 2a)+\sin 2a\cos a-\cos a=0\)

\(\Leftrightarrow \sin a.2\cos ^2a+\sin 2a\cos a-\cos a=0\)

\(\Leftrightarrow \cos a(2\sin 2a-1)=0\)

\(\Rightarrow \left[\begin{matrix} \cos a=0(1)\\ \sin 2a=\frac{1}{2}(2)\end{matrix}\right.\)

Từ (1)\(\Rightarrow a=\frac{\pi}{2}+k\pi \Rightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)

Từ (2) \(\Rightarrow \left[\begin{matrix} 2a=\frac{\pi}{6}+2k\pi \rightarrow x=\frac{\pi}{24}+\frac{k\pi}{2}\\ 2a=\frac{5\pi}{6}+2k\pi \rightarrow x=\frac{5\pi}{24}+\frac{k\pi}{2}\end{matrix}\right.\)