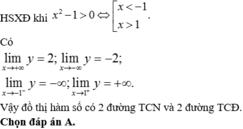Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y=(2x+3)/(x^2-1)
1M
Những câu hỏi liên quan
Xét các mệnh đề sau(1). Đồ thị hàm số
y
1
2
x
-
3
có hai đường tiệm cận đứng và một đường tiệm cận ngang(2). Đồ thị hàm số
y
x
+
x
2
+
x
+
1...
Đọc tiếp
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
Đúng 0
Bình luận (0)
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
2
x
-
1
x
2
-
1
là A. 4. B. 3. C. 1. D. 2.
Đọc tiếp
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = 2 x - 1 x 2 - 1 là
A. 4.
B. 3.
C. 1.
D. 2.
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
1
−
2
x
−
x
+
2
là: A.
x
−
2
;
y
−
2
B.
x
2
;
y
−...
Đọc tiếp
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 − 2 x − x + 2 là:
A. x = − 2 ; y = − 2
B. x = 2 ; y = − 2
C. x = − 2 ; y = 2
D. x = 2 ; y = 2
Đáp án là D.
Đồ thị có tiệm cận đứng và tiệm cận ngang lần lượt là: x = 2 ; y = 2.
Đúng 0
Bình luận (0)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2 x + 1 4 - x 2 là:
A. 2
B. 1
C. 3
D. 4
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 10 − 2 x x 2 + 2 x − 35
A. 1
B. 2
C. 3
D. 4
Đáp án C
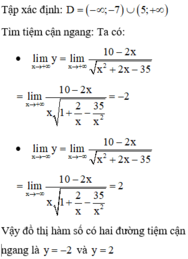
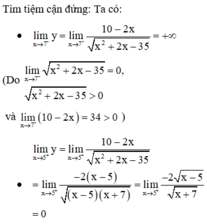
Vậy đồ thị hàm số có một đường tiệm cận đứng là x = -7
Lưu ý: HS có thể sử dụng MTCT để tính nhanh các bài toán tìm lim trên (tuy nhiên nên xem lại cách giải tự luận này khi gặp những bài toán không dùng MTCT được nữa).
Đúng 0
Bình luận (0)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = \(\dfrac{x+\sqrt{x^2+1}}{x+1}\)
Lời giải:
TXĐ: \((-\infty; -1)\cup (-1;+\infty)\)
\(\lim\limits_{x\to +\infty}y=\lim\limits_{x\to +\infty}\frac{1+\sqrt{1+\frac{1}{x}}}{1+\frac{1}{x}}=\frac{1+1}{1}=2\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to -\infty}\frac{-1+\sqrt{1+\frac{1}{x^2}}}{-1+\frac{1}{-x}}=\frac{-1+1}{-1}=0\)
Do đó ĐTHS có 2 TCN là $y=0$ và $y=2$
\(\lim\limits_{x\to -1-}y=\lim\limits_{x\to -1-}\frac{x+\sqrt{x^2+1}}{x+1}=-\infty\) do \(\lim\limits_{x\to -1-}(x+\sqrt{x^2+1})=\sqrt{2}-1>0\) và \(\lim\limits_{x\to -1-}\frac{1}{x+1}=-\infty\)
Tương tự \(\lim\limits_{x\to -1+}y=+\infty\) nên $x=-1$ là TCĐ của đths
Vậy có tổng 3 TCN và TCĐ
Đúng 1
Bình luận (0)
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
y
x
+
3
x
-
1
x
2
-
1
là A. 1. B. 2. C. 3 D. 4.
Đọc tiếp
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = x + 3 x - 1 x 2 - 1 là
A. 1.
B. 2.
C. 3
D. 4.
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
y
2
x
-
1
x
+
1
A. x -1;y2. B. x1;y -2. C. x1/2;y -1. D. x -1;y1/2.
Đọc tiếp
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = 2 x - 1 x + 1
A. x= -1;y=2.
B. x=1;y= -2.
C. x=1/2;y= -1.
D. x= -1;y=1/2.
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
y
2
x
-
1
x
+
1
A.
x
1
2
,
y
-
1
B.
x
1
,
y
-
2
C.
x
-...
Đọc tiếp
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = 2 x - 1 x + 1
A. x = 1 2 , y = - 1
B. x = 1 , y = - 2
C. x = - 1 , y = 2
D. x = - 1 , y = 1 2
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
y
2
x
-
1
x
+
1
A. ; . B. ; . C. ; . D. ; .
Đọc tiếp
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = 2 x - 1 x + 1
A. ![]() ;
; ![]() .
.
B. ![]() ;
; ![]() .
.
C. ![]() ;
; ![]() .
.
D. ![]() ;
; ![]() .
.