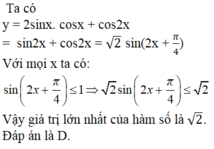Lời giải:
PT $\Leftrightarrow 1+2\sin x\cos x=\sin x+1-2\sin ^2x$

$\Leftrightarrow 2\sin x\cos x-\sin x+2\sin ^2x=0$

$\Leftrightarrow \sin x(2\cos x-1+2\sin x)=0$

Nếu $\sin x=0\Rightarrow x=k\pi$ với $k$ nguyên.

Nếu $2\cos x-1+2\sin x=0$

$\Leftrightarrow 2\cos x=1-2\sin x$

$\Rightarrow 4\cos ^2x=1+4\sin ^2x-4\sin x$

$\Rightarrow 4(1-\sin ^2x)=1+4\sin ^2x-4\sin x$
$\Leftrightarrow 8\sin ^2x-4\sin x-3=0$

Đến đây thì đơn giản rồi vì là pt bậc 2 1 ẩn $\sin x$

Phương trình:

3   sin 2 x + 2 sin x cos x - cos 2 x = 0 (*).

cos x = 0 ⇒   sin 2 x = 1  không phải là nghiệm của phương trình (*).

cos x ≠ 0 . Ta có: 

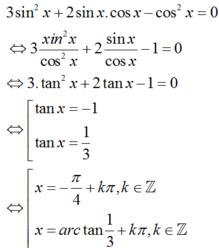
Nghiệm nguyên dương nhỏ nhất của phương trình là   x 0 ∈ 0 ; π 2

Chọn C.

\(y=\sqrt{3}cos2x+2sinxcosx-2\)

\(=\sqrt{3}cos2x+sin2x-2\)

Ta có: \(\left|\sqrt{3}cos2x+sin2x\right|\le\sqrt{\left(\sqrt{3}\right)^2+1^2}=2\)

Do đó \(-2\le\sqrt{3}cos2x+sin2x\le2\)

\(\Leftrightarrow-4\le\sqrt{3}cos2x+sin2x-2\le2\).

Ta có: \(\left|\sqrt{3}cosx-sinx\right|\le\sqrt{\left(\sqrt{3}\right)^2+\left(-1\right)^2}=2\)

Do đó \(-2\le\sqrt{3}cosx-sinx\le2\)

Pt \(\Leftrightarrow5cos^2x+2sinx.cosx-4\left(sin^2x+cos^2x\right)=0\)

\(\Leftrightarrow cos^2x+2sinx.cosx-4sin^2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=\left(-1-\sqrt{5}\right)sinx\\cosx=\left(-1+\sqrt{5}\right)sinx\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}cotx=-1-\sqrt{5}\\cotx=-1+\sqrt{5}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=arc.cot\left(-1-\sqrt{5}\right)+k\pi\\x=arc.cot\left(-1+\sqrt{5}\right)+k\pi\end{matrix}\right.\)(\(k\in Z\))

Vậy...

d la sai

(sin²x - 4cos²x)(sin²x - 2sinx.cosx) = 2cos⁴x

⇔ (5sin²x - 4)(sin²x - sin2x) = 2cos⁴x
⇔ \(\left(\dfrac{5-5cos2x}{2}-4\right)\left(\dfrac{1-cos2x}{2}-sin2x\right)\)= 2cos⁴x

⇔ \(\dfrac{5-5cos2x-8}{2}.\dfrac{1-cos2x-2sin2x}{2}\) = 2cos⁴x

⇔ (5cos2x + 3)(cos2x + 2sin2x - 1) = 8cos⁴x

⇔ 5cos²2x + 5cos2x.sin2x + 3cos2x + 6sin2x - 3 = 8cos⁴x

⇔ 5.\(\dfrac{1+cos4x}{2}\) + \(\dfrac{5}{2}sin4x\) + 3cos2x + 6sin2x - 3 = 8cos⁴x

⇔ \(\dfrac{5}{2}cos4x+\dfrac{5}{2}sin4x+3cos2x+6sin2x-\dfrac{1}{2}\) = 8cos⁴x

⇔ 5cos4x + 5sin4x + 6cos2x + 12sin2x - 1 = 16cos⁴x

VP = 16cos⁴x = 16 . \(\dfrac{\left(1+cos2x\right)^2}{4}\) = 4. (1 + cos2x)²

VP = 4 . (1 + 2cos2x + cos²2x)

VP = 4 + 8cos2x + 4 . \(\dfrac{1+cos4x}{2}\)

VP = 6 + 8cos2x+ 2cos4x

Vậy 3cos4x + 5sin4x - 2cos2x + 12sin2x - 7 = 0

@Nguyễn Việt Lâm giúp em với

đặt t=sinx+cosx và phải có đk của t

Đáp án B