Giúp em câu 4 và 5 ở bài 2 với ạ
CN
Những câu hỏi liên quan
 mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
mn giúp e câu C của bài 4 và 5 với ạ,em cảm ơn
Bài 4:
a) Thay x=49 vào B ta có:
\(B=\dfrac{1-\sqrt{49}}{1+\sqrt{49}}=-\dfrac{3}{4}\)
b) \(A=\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(A=\left[\dfrac{15-\sqrt{x}}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}+\dfrac{2\left(\sqrt{x}-5\right)}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\right]\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}+5\right)\left(\sqrt{x}-5\right)}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}-5}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(A=\dfrac{1}{\sqrt{x}+1}\)
c) Ta có:
\(M=A-B=\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{1-1+\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(M=\dfrac{\sqrt{x}+1-1}{\sqrt{x}+1}=\dfrac{\sqrt{x}+1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}=1-\dfrac{1}{\sqrt{x}+1}\)
Mà M nguyên khi:
\(1\) ⋮ \(\sqrt{x}+1\)
\(\Rightarrow\sqrt{x}+1\in\left\{1;-1\right\}\)
Mà: \(\sqrt{x}+1\ge1\)
\(\Rightarrow\sqrt{x}+1=1\)
\(\Rightarrow\sqrt{x}=0\)
\(\Rightarrow x=0\left(tm\right)\)
Vậy M nguyên khi x=0
Đúng 1
Bình luận (0)
Dạ mọi người giúp em bài 4 và câu 2 trắc nghiệm với ạ

ủa bạn ơi mình chưa thấy câu hỏi của bạn
\(\rightarrow\) đăng lại nhé có khả năng mình sẽ giúp dù hơi bận
Đúng 0
Bình luận (0)
Giúp em câu 1b và bài 4 với ạ

1B:
a: Ta có: \(N=\sqrt{8}+\sqrt{32}+\sqrt{108}-\sqrt{27}\)
\(=2\sqrt{2}+4\sqrt{2}+6\sqrt{3}-3\sqrt{3}\)
\(=6\sqrt{2}+3\sqrt{3}\)
b: Ta có: \(M=\dfrac{2}{2+\sqrt{3}}-\dfrac{1}{2-\sqrt{3}}\)
\(=4-2\sqrt{3}-2-\sqrt{3}\)
\(=2-3\sqrt{3}\)
Đúng 2
Bình luận (0)
Giúp em bài 5 câu a và c với ạ em cảm ơn rất nhìu
a) \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^0\\sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow\widehat{C}=37^0\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}AB=BD\\AC=DC\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
=> BC là đường trung trực AD
\(\Rightarrow AD\perp BC\)
Áp dụng HTL trong tam giác BDC vuông tại D:
\(FB.FC=FD^2\Rightarrow4FB.FC=4FD^2=\left(2FD\right)^2=AD^2\)
Đúng 0
Bình luận (0)
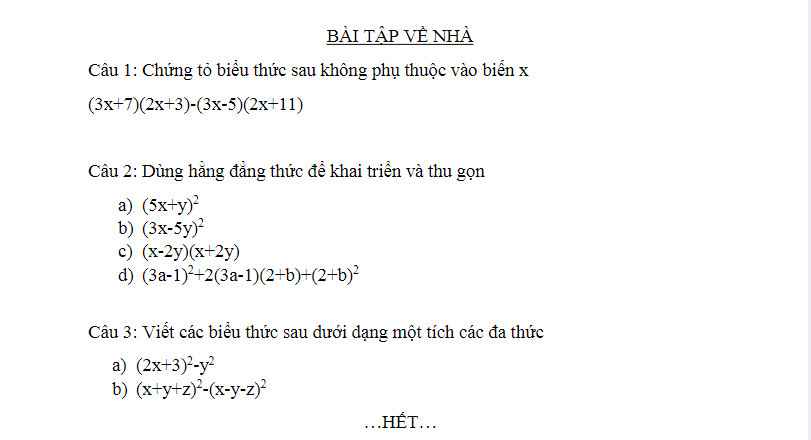
Câu 1:
Ta có: \(\left(3x+7\right)\left(2x+3\right)-\left(3x-5\right)\left(2x+11\right)\)
\(=6x^2+9x+14x+21-\left(6x^2+33x-10x-55\right)\)
\(=6x^2+23x+21-6x^2-23x+55\)
=76
Đúng 1
Bình luận (2)
giúp em câu 4 và câu 5 với ạ
Giúp em câu 2 bài 4 với ạ. Cần gấp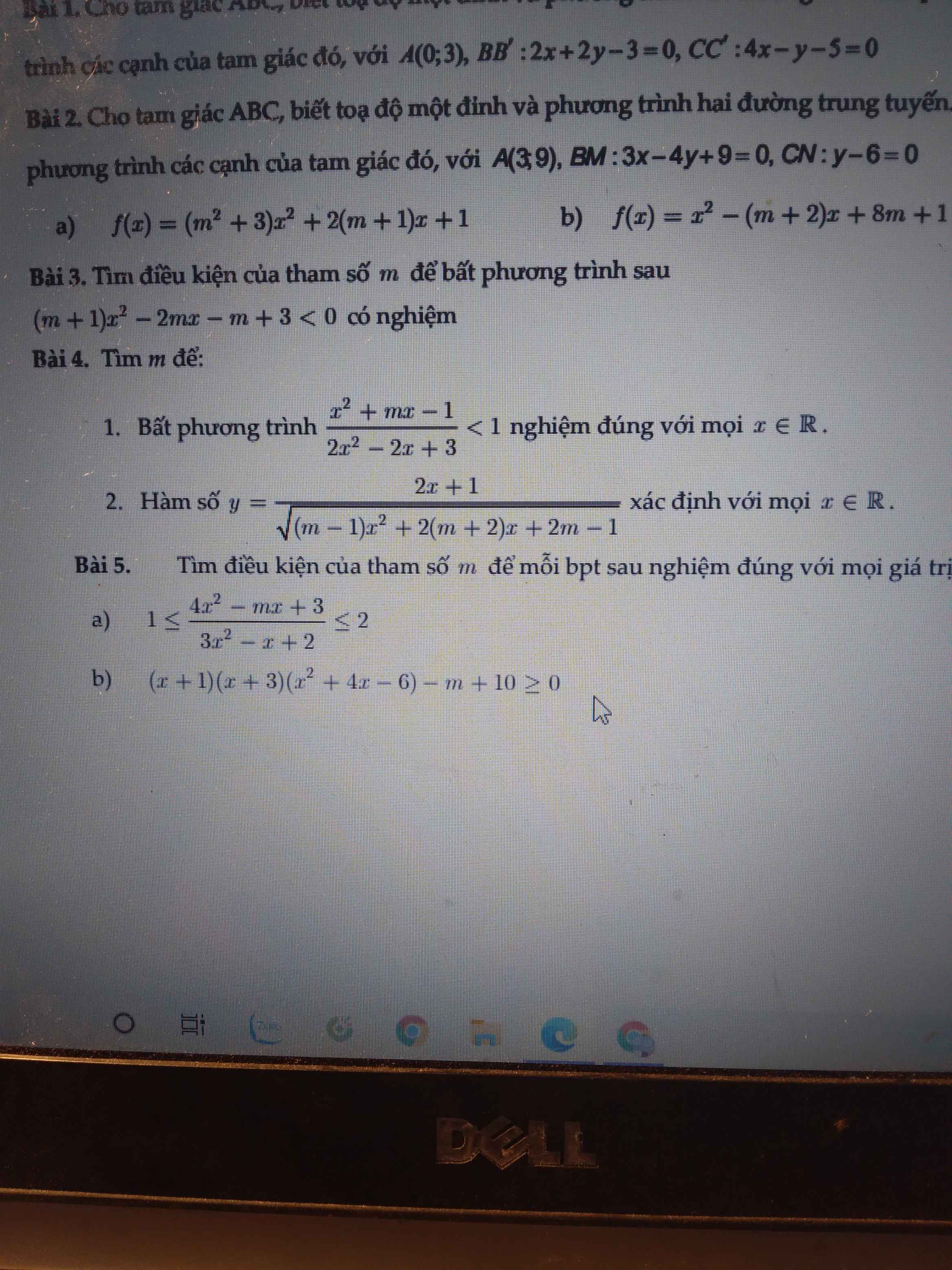
Dạ mng xem giúp mình mấy bài trắc nghiệm làm đúng chưa với ạ , mng giúp mình luôn câu 5 bài 2 và câu 2 bài 3 ạ
Mình cảm ơn trước ạ


Bài 2
5 C
Bài 3
1 D
6 C
Còn lại ol r nhé
Đúng 2
Bình luận (3)
Giúp em bài 4 và bài 5 với bài nào cũng được ạ.

Câu 5:
a: Ta có: \(A=\left(x-1\right)\left(x-3\right)+11\)
\(=x^2-4x+3+11\)
\(=x^2-4x+4+10\)
\(=\left(x-2\right)^2+10\ge10\forall x\)
Dấu '=' xảy ra khi x=2
b: Ta có: \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
Đúng 1
Bình luận (1)
Câu 5:
a) \(A=\left(x-1\right)\left(x-3\right)+11=x^2-4x+3+11\)
\(=x^2-4x+14\)
\(=\left(x^2-4x+4\right)+10=\left(x-2\right)^2+10\ge10\)
\(minA=10\Leftrightarrow x=2\)
b) \(B=3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)
Đúng 1
Bình luận (1)
GIÚP EM BÀI GIẢI PT VÀ CÂU C,D,E BÀI 2 VỚI Ạ..
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
Đúng 2
Bình luận (0)