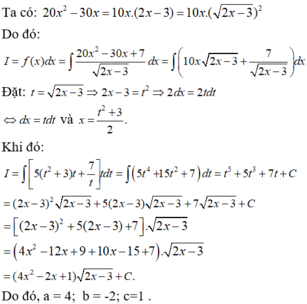với giá trị nào của a b c thì f(x) = g(x)
f(x) =x^ 3 + 1
g(x) = ( x + a ) (x^2 + bx +c )
LN
Những câu hỏi liên quan
Với giá trị nào của a, b thì đa thức f(x) chia hết cho đa thức g(x)
a) f(x) = x³ + ax² – 4. g(x) = x² + 4x + 4
b) f(x) = x⁴ + ax³ + bx – 1. g(x) = x² – 1
c) f(x) = 2x³ – 3ax² + 2x +b g(x) = (x – 1)(x + 2)
\(a,\Leftrightarrow f\left(x\right)⋮g\left(x\right)=\left(x+2\right)^2\\ \Leftrightarrow f\left(-2\right)=-8+4a-4=0\\ \Leftrightarrow a=3\\ b,\Leftrightarrow f\left(x\right)⋮g\left(x\right)=\left(x-1\right)\left(x+1\right)\\ \Leftrightarrow f\left(1\right)=f\left(-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}1+a+b-1=0\\1-a-b-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=0\\a+b=0\end{matrix}\right.\Leftrightarrow a,b\in R\\ \text{Vậy }f\left(x\right)⋮g\left(x\right),\forall a,b\\ c,\Leftrightarrow f\left(1\right)=f\left(-2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2-3a+2+b=0\\-18-12a-4+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3a-b=4\\12a-b=-22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{26}{9}\\b=-\dfrac{38}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
với giá trị nguyên nào của a,b,c thì f(x)=g(x)
biết:
\(f\left(x\right)=x^3+1\) ; \(g\left(x\right)=\left(x+a\right)\left(x^2+bx+c\right)\)
f(x)=x3+1=(x+1)(x2-x+1)
Mà f(x)=g(x)=(x+a)(x2+bx+c)
Nên: a=1;b=-1;c=1
Đúng 0
Bình luận (0)
ta có : f(x)=x3+1=(x+1)(x2-x+1).
lại có: g(x)=(x+a)(x2+bx+c)
để f(x)=g(x) thì (x+1)(x2-x+1)=(x+a)(x2+bx+c)
<=> \(\begin{cases}x+1=x+a\\x^2-x+1=x^2+bx+c\end{cases}\)
<=>\(\begin{cases}a=1\\b=-1\\c=1\end{cases}\)
vậy với a=1, b=-1 và c=1 thì f(x)=g(x)
Đúng 0
Bình luận (2)
Ta có:
g(x)=(x+a)(x2+bx+c)
=x3+bx2+cx+ax2+abx+ac
=x3+bx2+ax2+cx+abx+ac
=x3+(b+a)x2+(c+ab)x+ac
Đồng nhất đa thức g(x) với f(x)=x3+1,ta đc:
a+b=0
{ ab+c=0
ac=1 (xl vì mk ko viết dấu { được)
tới đây tự giải tiếp nhé,a=1;b=-1;c=1
Đúng 0
Bình luận (0)
1)cho f(x)ax^3+bx^2+cx+d trong đó a,b,c,d thuộc Z và thỏa mãn b3a+c.Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.2)cho đa thức f(x)ax^2+bx+c với a,b,c là hằng số.Hãy xác định a,b,c biết f(1)4,f(-1)8 và a-c43)cho f(x)ax^3+4x(x^2-1)+8;g(x)x^3-4x(bx-1)+c-3.Xác định a,b,c để f(x)g(x).4)cho f(x)cx^2+bx+a và g(x)ax^2+bx+c.cmr nếu Xo là nghiệm của f(x) thì 1/Xo là nghiệm của g(x)5)cho đa thức f(x) thỏa mãn xf(x+2)(x^2-9)f(x).cmr đa thức f(x) có ít nhất 3 nghiệm6)tính f(2) biết f(x)+(x+1)...
Đọc tiếp
1)cho f(x)=ax^3+bx^2+cx+d trong đó a,b,c,d thuộc Z và thỏa mãn b=3a+c.Chứng minh rằng f(1).f(-2) là bình phương của một số nguyên.
2)cho đa thức f(x)=ax^2+bx+c với a,b,c là hằng số.Hãy xác định a,b,c biết f(1)=4,f(-1)=8 và a-c=4
3)cho f(x)=ax^3+4x(x^2-1)+8;g(x)=x^3-4x(bx-1)+c-3.Xác định a,b,c để f(x)=g(x).
4)cho f(x)=cx^2+bx+a và g(x)=ax^2+bx+c.
cmr nếu Xo là nghiệm của f(x) thì 1/Xo là nghiệm của g(x)
5)cho đa thức f(x) thỏa mãn xf(x+2)=(x^2-9)f(x).cmr đa thức f(x) có ít nhất 3 nghiệm
6)tính f(2) biết f(x)+(x+1)f(-x)=x+2
Cho các đa thức: f(x)=ax^2+bx+c(a,b,c là các hằng số) và g(x)= (2009x+2010)^2. Tính a-b+c nếu biết f(x)=g(x) với mọi giá trị của biến x
Cho các hàm số:
f
(
x
)
20
x
2
-
30
x
+
7
2
x
-
3
;
F
(
x
)
(
a
x
2
+
b...
Đọc tiếp
Cho các hàm số: f ( x ) = 20 x 2 - 30 x + 7 2 x - 3 ; F ( x ) = ( a x 2 + b x + C ) 2 x - 3 với x > 3 2 . Để F(x) là một nguyên hàm của f(x) thì giá trị của a,b,c lần lượt là:
A. a = 4; b = 2; c= 1
B. a = 4; b = -2; c = -1
C. a = 4; b = -2; c = 1
D. a = 4; b = 2; c = -1 .
f(x) = 3x^2 - x^3 +2x +4 +6x^3
g(x)= -x+5x^3-4x^2+8
a. Thu gọn và tìm bậc của 2 đa thức
b. Tìm A(x)= f(x) +g(x) và B(x) = f(x) -g(x)
c. Với x=1; -1 thì giá trị nào là nghiệm của B(x)
biết đa thức f(x)=ax^2+bx+c có gia trị nguyên với mọi giá trị của x.CMR
a) c và 2a là các số nguyên
b)khi a =1;b=3;c=4 thì ko có số nguyên x nào để f(x)=2017
biết đa thức f(x)=ax2+bx+c có giá trị nguyên với mọi giá trị của x . chứng minh rằng
a) c và 2a là các số nguyên
b) khi a =1 ;b=3;c=4 thì không có số nguyên x nào để f(x)=2017
cho 1 like cho ai giải được
cho các số thực a, b, c và đa thức g(x)=x^3 + ax^2 + x + 10 có 3 nghiệm phân biệt. Biết rằng mỗi nghiệm của đa thức g(x) lại là nghiệm của đa thức f(x)=x^4 + x^3 + bx^2 + 100x + c. Tính giá trị của f(1)