Cho an = 1+2+3+...+n. Chứng minh rằng an+an+1 là một số chính phương
H24
Những câu hỏi liên quan
Chứng Minh: Với mọi số tự nhiên n thì an=n(n+1)(n+2)(n+3)+1 là số chính phương
Ta có:
an = n(n+1)(n+2)(n+3) + 1
= (n2 + 3n)(n2 + 3n + 2) +1
= (n2 + 3n)2+ 2(n2 + 3n) + 1
= (n2 + 3n + 1)2
Với n là số tự nhiên thì (n2 + 3n + 1)2 cũng là số tự nhiên, vì vậy, an là số chính phương.
Chứng minh : Với mọi số tự nhiên n thì an = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương.
Ta có:
an = n(n+1)(n+2)(n+3) + 1
= (n2 + 3n)(n2 + 3n + 2) +1
= (n2 + 3n)2+ 2(n2 + 3n) + 1
= (n2 + 3n + 1)2
Với n là số tự nhiên thì (n2 + 3n + 1)2 cũng là số tự nhiên, vì vậy, an là số chính phương.
Bài toán 1 : Chứng minh : Với mọi số tự nhiên n thì an = n(n + 1)(n + 2)(n + 3) + 1 là số chính phương.
Ta có:
an = n(n+1)(n+2)(n+3) + 1
= (n2 + 3n)(n2 + 3n + 2) +1
= (n2 + 3n)2+ 2(n2 + 3n) + 1
= (n2 + 3n + 1)2
Với n là số tự nhiên thì (n2 + 3n + 1)2 cũng là số tự nhiên, vì vậy, an là số chính phương.
cho dãy số:1,1,2,3,5,8,13,.... trong đó mỗi số hạng, kể từ số thứ 3, bằng tổng của 2 số hạng đứng liền trước. Chứng minh rằng an-1+an+1/an+an+2 là phân số tối giản với mọi n>=2
đề thấy hơi chán,từ số kia =2an,mẫu số cx chia hết cho 2 thì sao tối giản đc hả bạn ơi
Đúng 0
Bình luận (0)
Cho dãy số (an) xác định bởi: a1=5; an= an-1 + 3n ∀ n ≥ 2. Chứng minh dãy số bn= an+1 - an ∀ n ≥ 2 là một cấp số cộng.
1) Tồn tại hay không số nguyên x thỏa mãn 202x + 122x + 20152x là một số chính phương.
2) Cho n là một số nguyên dương và n số nguyên dương a1 , a2 , a3 , …, an có tổng bằng 2n - 1. Chứng minh rằng tồn tại một số số trong n số đã cho có tổng bằng n.
20^2x có tận cùng là 0
12^2x=144^x;2012^2x=4048144^x
xét x=2k+1 thì ta có: 144^(2k+1)=144^2k*144=20726^k*144 có tận cùng là 4
4048144^(2k+1)=(...6)^2*4048144 có tận cùng là 4
suy ra số đã cho có tận cùng là 8 không phải là số chính phương (1)
xét x=2k thì ta có:144^2k=20736^k có tận cùng là 6
4948144^2k=(...6)^k có tận cùng là 6
suy ra số đã cho có tận cùng là 2 không phải là số chính phương (2)
từ(1) và (2) suy ra không tồn tại số x
Đúng 0
Bình luận (0)
Đinh Tuấn việt chép mạng thề luôn!
nếu x = 2k thì 2015^2x = 4060225^x chứ không phải là 4048144^x nha
Nếu mún bt hãy xem dòng thứ 2 của lời giải của bạn ấy có ghi là
2012^2x = 4048144^x
Nhưng đề bài lại nói là 2015^2x cơ mà ??
Đúng 0
Bình luận (0)
1.Cho n >= 2. Chứng minh rằng tồn tại các số a1<a2<a3<...<an; a nguyên dương sao cho
1/a1^2 + 1/a2^2 +...+ 1/an^2 = 1/a^2
2.Cho 7 số tự nhiên phân biệt có tổng là 100. Chứng minh tồn tại 3 số có tổng lớn hơn hoặc bằng 50
Hai bạn Bình và An mỗi bạn viết ra một số. Lấy số của Bình viết cộng thêm 1 rồi nhân với số của An thì được một số là số chính phương. Lấy số của An cộng thêm 1 rồi nhân với số của Bình thì ta được một số là số chính phương. Nếu cho số của Bình là 8 còn số của An viết là một số nguyên lớn 1, nhỏ hơn 100 thì số An viết ra là số nào
Chứng minh phương trình luôn
x
n
+
a
1
x
n
-
1
+
a
2
x
n
-
2
+
....
Đọc tiếp
Chứng minh phương trình luôn x n + a 1 x n - 1 + a 2 x n - 2 + . . . + a n - 1 x + a n = 0 có nghiệm với n là số tự nhiên lẻ.
Hàm số f ( x ) = x n + a 1 x n - 1 + a 2 x n - 2 + . . . + a n - 1 x + a n = 0 xác định trên R
- Ta có
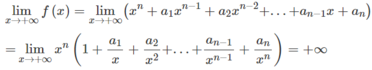
Vì 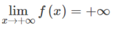 nên với dãy số
(
x
n
)
bất kì mà
x
n
→
+
∞
ta luôn có lim
f
(
x
n
)
=
+
∞
nên với dãy số
(
x
n
)
bất kì mà
x
n
→
+
∞
ta luôn có lim
f
(
x
n
)
=
+
∞
Do đó, f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại số a sao cho f(a) > 1 (1)
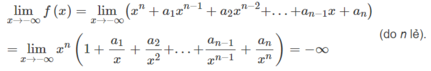
Vì 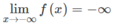 nên với dãy số
(
x
n
)
bất kì mà
x
n
→
−
∞
ta luôn có lim
f
(
x
n
)
=
−
∞
hay
l
i
m
[
−
f
(
x
n
)
]
=
+
∞
nên với dãy số
(
x
n
)
bất kì mà
x
n
→
−
∞
ta luôn có lim
f
(
x
n
)
=
−
∞
hay
l
i
m
[
−
f
(
x
n
)
]
=
+
∞
Do đó, − f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì − f ( x n ) > 1 kể từ số hạng nào đó trở đi. Nói cách khác, luôn tồn tại b sao cho −f(b) > 1 hay f(b) < −1 (2)
- Từ (1) và (2) suy ra f(a).f(b) < 0
Mặt khác, f(x) hàm đa thức liên tục trên R nên liên tục trên [a; b]
Do đó, phương trình f(x) = 0 luôn có nghiệm.
Đúng 0
Bình luận (0)
Cho \(a_n=1+2+3+...+n\). Chứng minh rằng \(a_n+a_{n+1}\) là một số chính phương.
\(a_n=1+2+3+...+n=\dfrac{n\left(n+1\right)}{2}\)
\(\Rightarrow a_{n+1}=1+2+3+...+n+\left(n+1\right)=\dfrac{\left(n+1\right)\left(n+2\right)}{2}\)
\(\Rightarrow a_n+a_{n+1}=\dfrac{n\left(n+1\right)}{2}+\dfrac{\left(n+1\right)\left(n+2\right)}{2}\)
\(=\dfrac{\left(n+1\right)}{2}.\left(n+n+2\right)=\dfrac{\left(n+1\right)}{2}.\left(2n+2\right)\)
\(=\dfrac{\left(n+1\right)}{2}.2\left(n+1\right)=\left(n+1\right)^2\)
\(\Rightarrow dpcm\)
Đúng 1
Bình luận (0)



