Hàm số f ( x ) = x n + a 1 x n - 1 + a 2 x n - 2 + . . . + a n - 1 x + a n = 0 xác định trên R
- Ta có
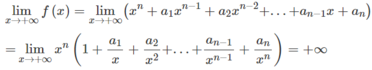
Vì 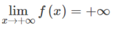 nên với dãy số
(
x
n
)
bất kì mà
x
n
→
+
∞
ta luôn có lim
f
(
x
n
)
=
+
∞
nên với dãy số
(
x
n
)
bất kì mà
x
n
→
+
∞
ta luôn có lim
f
(
x
n
)
=
+
∞
Do đó, f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì f ( x n ) > 1 kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại số a sao cho f(a) > 1 (1)
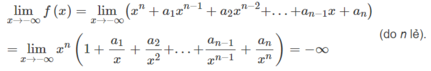
Vì 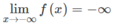 nên với dãy số
(
x
n
)
bất kì mà
x
n
→
−
∞
ta luôn có lim
f
(
x
n
)
=
−
∞
hay
l
i
m
[
−
f
(
x
n
)
]
=
+
∞
nên với dãy số
(
x
n
)
bất kì mà
x
n
→
−
∞
ta luôn có lim
f
(
x
n
)
=
−
∞
hay
l
i
m
[
−
f
(
x
n
)
]
=
+
∞
Do đó, − f ( x n ) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì − f ( x n ) > 1 kể từ số hạng nào đó trở đi. Nói cách khác, luôn tồn tại b sao cho −f(b) > 1 hay f(b) < −1 (2)
- Từ (1) và (2) suy ra f(a).f(b) < 0
Mặt khác, f(x) hàm đa thức liên tục trên R nên liên tục trên [a; b]
Do đó, phương trình f(x) = 0 luôn có nghiệm.


