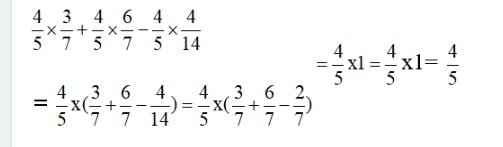(7+X)x4+X=108 cách giải
NA
Những câu hỏi liên quan
{7+X}x4+x=108
( 7 + x ) * 4 + x = 108
=> 28 + 4x + x = 108
=> 28 + 5x = 108
=> 5x = 80
=> x = 16 (tm)
Đúng 0
Bình luận (0)
(7 + x ) * 4 + x = 108
7 * 4 + x * 4 + x = 108
28 + x * 5 = 108
x * 5 = 108 - 28
x * 5 = 80
x = 80 : 5
x = 16
Đúng 0
Bình luận (0)
( 7 + x ) x 4 + x = 108
7 x 4 + x x 4 + x = 108
28 + x x 5 = 108
x x 5 = 108 - 28
x x 5 = 80
x = 80 : 5
x = 16
Đúng 0
Bình luận (0)
{7+X}X4+X=108
(7+X)x4+X=108
=> 28+4X+X=108
=> 5X=108-28
=> 5X =80
=> X=16
tính bằng cách thuận tiện nhất:
4/5 x 3/7 x 4/5 x 6/7 x 4/5 x4/14(giúp với)
\(\dfrac{4}{5}\times\dfrac{3}{7}\times\dfrac{4}{5}\times\dfrac{6}{7}\times\dfrac{4}{14}=\dfrac{4}{5}\times\dfrac{3}{7}+\dfrac{4}{5}\times\dfrac{6}{7}-\dfrac{4}{5}\times\dfrac{2}{7}=\dfrac{4}{5}\times\left(\dfrac{6}{7}+\dfrac{3}{7}-\dfrac{2}{7}\right)=\dfrac{4}{5}\)
Đúng 1
Bình luận (0)
tính cách thuận tiện nhất 15,8 x 108 - 15,8 x 7 -15,8
=15,8 x (108 - 7)
=15,8 x 101
=
Đúng 0
Bình luận (0)
`15,8xx108-15,8xx7-15,8`
`=15,8xx(108-7-1)`
`=15,8xx100`
`=1580`
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
108.
a) x=105
b) x=134
các bạn giải nhanh giúp mk( ghi ra luôn cách giải)
tính bằng cách thuận tiện nhất
a) 4 giờ 22 phút x 4 + 5 giờ 38 phút x4
b) 7 phút 30 giây x 7 - 6 phút 30 giây x 7
a) 4 giờ 22 phút x 4 + 5 giờ 38 phút x 4
= ( 4 giờ 22 phút + 5 giờ 38 phút ) x 4
= 10 giờ x 4
=40 giờ
b) 7 phút 30 giây x 7 - 6 phút 30 giây x 7
= ( 7 phút 30 giây - 6 phút 30 giây ) x 7
= 1 phút x 7
= 7 phút
Kết bn với mik nha!
Đúng 0
Bình luận (0)
Cho 3 đa thức: A(x)= -7+2x2+x4+3x5-x3
B(x)= -x+x4+2x3-7
C(x)= 2x-x4-3x3
Tính A(x)+B(x)-C(x)
\(A\left(x\right)+B\left(x\right)-C\left(x\right)\)
\(=\left(-7+2x^2+x^4+3x^5-x^3\right)+\left(-x+x^4+2x^3-7\right)-\left(2x-x^4-3x^3\right)\)
\(=3x^5+3x^4+4x^3+2x^2-3x-14\)
Đúng 0
Bình luận (0)
Giải các phương trình sau (Đặt ẩn phụ)
d) x(x+1)(x2+x+1)=42
e) (x-1)(x-3)(x+5)(x+7)-297=0
f) x4-2x2-144x-1295=0
d: \(x\left(x+1\right)\left(x^2+x+1\right)=42\left(1\right)\)
=>\(\left(x^2+x\right)\left(x^2+x+1\right)=42\)
Đặt \(a=x^2+x\)
Phương trình (1) sẽ trở thành \(a\left(a+1\right)=42\)
=>\(a^2+a-42=0\)
=>(a+7)(a-6)=0
=>\(\left(x^2+x+7\right)\left(x^2+x-6\right)=0\)
mà \(x^2+x+7=\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}>0\forall x\)
nên \(x^2+x-6=0\)
=>(x+3)(x-2)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=2\end{matrix}\right.\)
e: \(\left(x-1\right)\left(x-3\right)\left(x+5\right)\left(x+7\right)-297=0\left(2\right)\)
=>\(\left(x-1\right)\left(x+5\right)\left(x-3\right)\left(x+7\right)-297=0\)
=>\(\left(x^2+4x-5\right)\left(x^2+4x-21\right)-297=0\)
Đặt \(b=x^2+4x\)
Phương trình (2) sẽ trở thành \(\left(b-5\right)\left(b-21\right)-297=0\)
=>\(b^2-26b+105-297=0\)
=>\(b^2-26b-192=0\)
=>(b-32)(b+6)=0
=>\(\left(x^2+4x-32\right)\left(x^2+4x+6\right)=0\)
mà \(x^2+4x+6=\left(x+2\right)^2+2>0\forall x\)
nên \(x^2+4x-32=0\)
=>(x+8)(x-4)=0
=>\(\left[{}\begin{matrix}x+8=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\x=4\end{matrix}\right.\)
f: \(x^4-2x^2-144x-1295=0\)
=>\(x^4-7x^3+7x^3-49x^2+47x^2-329x+185x-1295=0\)
=>\(\left(x-7\right)\cdot\left(x^3+7x^2+47x+185\right)=0\)
=>\(\left(x-7\right)\left(x+5\right)\left(x^2+2x+37\right)=0\)
mà \(x^2+2x+37=\left(x+1\right)^2+36>0\forall x\)
nên (x-7)(x+5)=0
=>\(\left[{}\begin{matrix}x-7=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-5\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình
e) x4 -4x3-8x2+8x=0
f) 2x2+3xy+y2=0
g) 2x4-x3-9x2+13x-5=0
h) (x+1)(x+3)(x+5)(x+7)+15=0
e: =>x(x^3-4x^2-8x+8)=0
=>x[(x^3+8)-4x(x+2)]=0
=>x(x+2)(x^2-2x+4-4x)=0
=>x(x+2)(x^2-6x+4)=0
=>\(x\in\left\{0;-2;3+\sqrt{5};3-\sqrt{5}\right\}\)
g: =>2x^4+5x^3-6x^3-15x^2+6x^2+15x-2x-5=0
=>(2x+5)(x^3-3x^2+3x-1)=0
=>(2x+5)(x-1)^3=0
=>x=1 hoặc x=-5/2
h: =>(x^2+8x+7)(x^2+8x+15)+15=0
=>(x^2+8x)^2+22(x^2+8x)+120=0
=>(x^2+8x+10)(x^2+8x+12)=0
=>(x^2+8x+10)(x+2)(x+6)=0
=>\(x\in\left\{-2;-6;-4+\sqrt{6};-4-\sqrt{6}\right\}\)
Đúng 0
Bình luận (0)