
mọi người giúp mình câu a với ạ
Mọi người giúp mình câu 6,7,9,11 với
Mấy câu đã làm câu nào sai sửa giúp mình với
Cám ơn mọi người nhìu lắm ạ❤
Mọi người ơi giúp mình 2 câu này với ạ. Mình cảm ơn mọi người rất nhiều ạ 
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

mọi người giúp mình câu 3 câu 4 với ạ
mình đang cần gấp cám ơn mọi người

mọi người giúp mình giải hết các câu a,b,c với ạ
mình đang cần gấp mình cám ơn ạ
Mọi người giúp mình bài 8 và bài 9 câu a với ạ 
8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)
Mọi người ơi, giúp mình điền vào chỗ trống câu này với ạ. Cảm ơn mọi người ạ.

Mọi người giúp mình câu này với ạ. Mình đang cần gấp ạ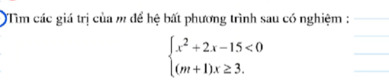
Mọi người ơi, giúp mình giải câu 3 và câu 4 của phần đọc hiểu trong ảnh với ạ! Mỗi câu mọi người trả lời bằng các gạch đầu dòng mọi người nhé! Mình xin cảm ơn nhiều ạ! 🙇♀️🙇♂️
Câu 4 ạ. Mọi người giúp mình nhanh với ạ
Câu 4:
PTHH: \(Zn+S\underrightarrow{t^o}ZnS\)
Ta có: \(\left\{{}\begin{matrix}n_{Zn}=\dfrac{0,65}{65}=0,01\left(mol\right)\\n_S=\dfrac{0,384}{32}=0,012\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\) Lưi huỳnh còn dư, Kẽm p/ứ hết
\(\Rightarrow\left\{{}\begin{matrix}n_{ZnS}=0,01\left(mol\right)\\n_{S\left(dư\right)}=0,002\left(mol\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m_{ZnS}=0,01\cdot97=0,97\left(g\right)\\m_{S\left(dư\right)}=0,002\cdot32=0,064\left(g\right)\end{matrix}\right.\)
Câu 4: (Bonus)
Ta có: \(n_{FeS}=\dfrac{17,6}{88}=0,2\left(mol\right)\)
Bảo toàn nguyên tố Lưu huỳnh: \(n_{FeS}=n_{PbS}=0,2\left(mol\right)\)
\(\Rightarrow m_{PbS}=0,2\cdot239=47,8\left(g\right)\)