a)

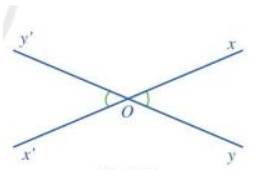
b)

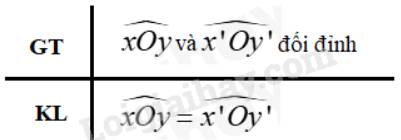
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau

\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù

\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)

\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)

khó thì 10 like cũng ko được nữa là 1 like

a)

giả thiết vs kết luận bạn tự ghi nha, có đó dễ.

c/m:

gọi x và y là số đo góc tạo bởi 2 tia phân giác của 2 góc kề bù.

ta có: 2x + 2y= 180 độ

suy ra x+y = 180/2=90 độ

Bài 1 :

Giả thiết : Góc tạo bởi hai tia phân giác của 2 góc kề bù

Kết luận : là 1 góc vuông

Chứng minh :

gọi x và y là số đo góc tạo bởi 2 tia phân giác của 2 góc kề bù.

ta có: 2x + 2y= 180 độ

suy ra x+y = \(\dfrac{180^o}{90^o}\)=90 độ

Bài 2:

Giả thiết: Nếu một đường thẳng cắt 2 đường thẳng phân biệt trogn số các góc tạo thành có một cặp góc so le trong bằng nhau

Kết luận: thì các cặp góc đồng vị bằng nhau.

Hướng dẫn nha:

Bạn vẽ hai đường thẳng phân biệt song song vs nhau

Vẽ một đường thẳng bất kì đi qua 2 đưuòng thẳng song song đó.

Khi đó sẽ tạo thành hai cặp góc so le trong và đồng vị bằng nhau.

Mik ghi nhầm 180° nha

Giả thiết: ΔABC

Kết luận: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)

- Gỉa thiết: Một đường thẳng cắt 2 đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau

- Kết luận: Các góc đồng vị bằng nhau

giả thiết luôn luôn đứng trước chữ thì còn kết luận sẽ đứng sau chữ thì ok bạn vẽ hình ra tìm đâu là cặp góc SlT rồi chứng minh nó bằng nhau thì ta suy ra đc các góc đồng vị bằng nhau trong sách hình như có hướng dẫn mà

Cho định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau

- Hãy cho biết giả thuyết của định lí đó

- Hãy cho biết kết luận của định lí đó

- Hãy chứng minh định lí đó

Được cập nhật Hôm qua lúc 20:29