Trong mặt phẳng tọa độ xOy, cho các điểm A', B' lần lượt là ảnh của các điểm A(2;3), B(1;1) qua phép tịnh tiến theo vectơ v(3;1). Tính độ dài vectơ A',B' A.2 B√3 C.√5 D√2
H24
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P). A.
3
x
+
2
y
+
z
+
14
0
B.
2
x
+
y
+
3
z
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Đáp án A.
Ta có A M ⊥ B C ⊥ O A ⇒ B C ⊥ O A M ⇒ B C ⊥ O M
Tương tự ta cũng có O M ⊥ A C ⇒ O M ⊥ P ⇒ P (P) nhận O M ¯ = 3 ; 2 ; 1 là vecto pháp tuyến.
Trong các đáp án, chọn đáp án mặt phẳng có vecto pháp tuyến có cùng giá với O M ¯ và không chứa điểm M thì thỏa.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
+
2
y
+
3
z
0
. Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phư...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x + 2 y + 3 z = 0 . Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
−
2
x
+
2
y
+
3
z
0
. Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 − 2 x + 2 y + 3 z = 0 . Các điểm A, B, C lần lượt là giao điểm (khác gốc tọa độ) của mặt cầu (S) và các trục tọa độ Ox, Oy, Oz. Phương trình mặt phẳng (ABC) là
A. 6 x − 3 y − 2 z − 12 = 0
B. 6 x + 3 y + 2 z − 12 = 0
C. 6 x − 3 y − 2 z + 12 = 0
D. 6 x − 3 y + 2 z − 12 = 0
Đáp án A.
6 x - 3 y + 2 z - 12 = 0 .
Tương tự
B 0 ; 4 ; 0 , C 0 ; 0 ; 6 ⇒ A B C : x 2 + y 4 + z 6 = 1 ⇔ 6 x + 3 y + 2 z − 12 = 0.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P). A. 3x+2y+z+140 B. 2x+y+3z+90 C. 3x+2y+z-140 D. 2x+y+z-90.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3x+2y+z+14=0
B. 2x+y+3z+9=0
C. 3x+2y+z-14=0
D. 2x+y+z-9=0.
Chọn A
Gọi A(a;0;0);B(0;b;0);C(0;0;c)
Phương trình mặt phẳng (P) có dạng:
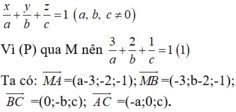
Vì M là trực tâm của tam giác ABC nên:
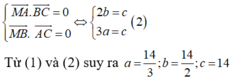
Khi đó phương trình (P): 3x+2y+z-14=0.
Vậy mặt phẳng song song với (P) là: 3x+2y+z+14=0.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxy cho mặt phẳng
α
:
2
x
-
y
-
3
z
4
. Gọi A ,B ,C lần lượt là giao điểm của mặt phẳng
α
với các trục tọa độ Ox, Oy, Oz. Thể tích tứ diện OABC bằng: A. 1. B. 2. C.
32
9
D.
16
9
Đọc tiếp
Trong không gian với hệ tọa độ Oxy cho mặt phẳng α : 2 x - y - 3 z = 4 . Gọi A ,B ,C lần lượt là giao điểm của mặt phẳng α với các trục tọa độ Ox, Oy, Oz. Thể tích tứ diện OABC bằng:
A. 1.
B. 2.
C. 32 9
D. 16 9
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức
-
1
+
3
i
1
-
i
;
5
i
1
+
2
i
;
3
i
. Khi đó tam giác ABC: A. Vuông tại A....
Đọc tiếp
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức - 1 + 3 i 1 - i ; 5 i 1 + 2 i ; 3 i . Khi đó tam giác ABC:
A. Vuông tại A.
B. Vuông cân tại C.
C. Tam giác đều
D. Vuông tại C.
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức
-
1
+
3
i
1
-
i
,
5
i
1
+
2
i
,
3
i
. Khi đó tam giác ABC A. Vuôn...
Đọc tiếp
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức - 1 + 3 i 1 - i , 5 i 1 + 2 i , 3 i . Khi đó tam giác ABC
A. Vuông tại A.
B. Vuông cân tại C
C. Tam giác đều
D. Vuông tại C.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là: A.
x
-
2
+
y
-
1
+
z
3
1
B.
x
-
2
+...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
A. x - 2 + y - 1 + z 3 = 1
B. x - 2 + y - 1 + z 3 = 0
C. x 2 + y 1 + z - 3 = 1
D. x 2 + y 1 + z - 3 = 0
Chọn đáp án A
Hình chiếu của A x 0 ; y 0 ; z 0 lên các trục Ox, Oy, Oz lần lượt là các điểm A1 ( x 0 ;0;0), A2 (0; y 0 ;0), A3 (0;0; z 0 ).
Do đó hình chiếu của M (-2;-1;3) lên các trục Ox, Oy, Oz lần lượt là các điểm A (-2;0;0), B (0;-1;0), C (0;0;3).
Phương trình mặt phẳng theo đoạn chắn đi qua ba điểm A, B, C là: x - 2 + y - 1 + z 3 = 1
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm
M
1
;
2
;
3
và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC. A.
6
x
+
3
y
−
2
z
−
6
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M 1 ; 2 ; 3 và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6 x + 3 y − 2 z − 6 = 0
B. x + 2 y + 3 z − 14 = 0
C. x + 2 y + 3 z − 11 = 0
D. x 1 + y 2 + z 3 = 3
Đáp án B
Vì OA, OB, OC đôi một vuông góc và M là trực tâm Δ A B C ⇒ O M ⊥ A B C
Suy ra mp A B C nhận O M → làm véc tơ pháp tuyến và đi qua điểm M(1;2;3)
Vậy phương trình m p P : 1. x − 1 + 2. y − 2 + 3. z − 3 = 0 ⇔ x + 2 y + 3 z − 14 = 0
Đúng 0
Bình luận (0)