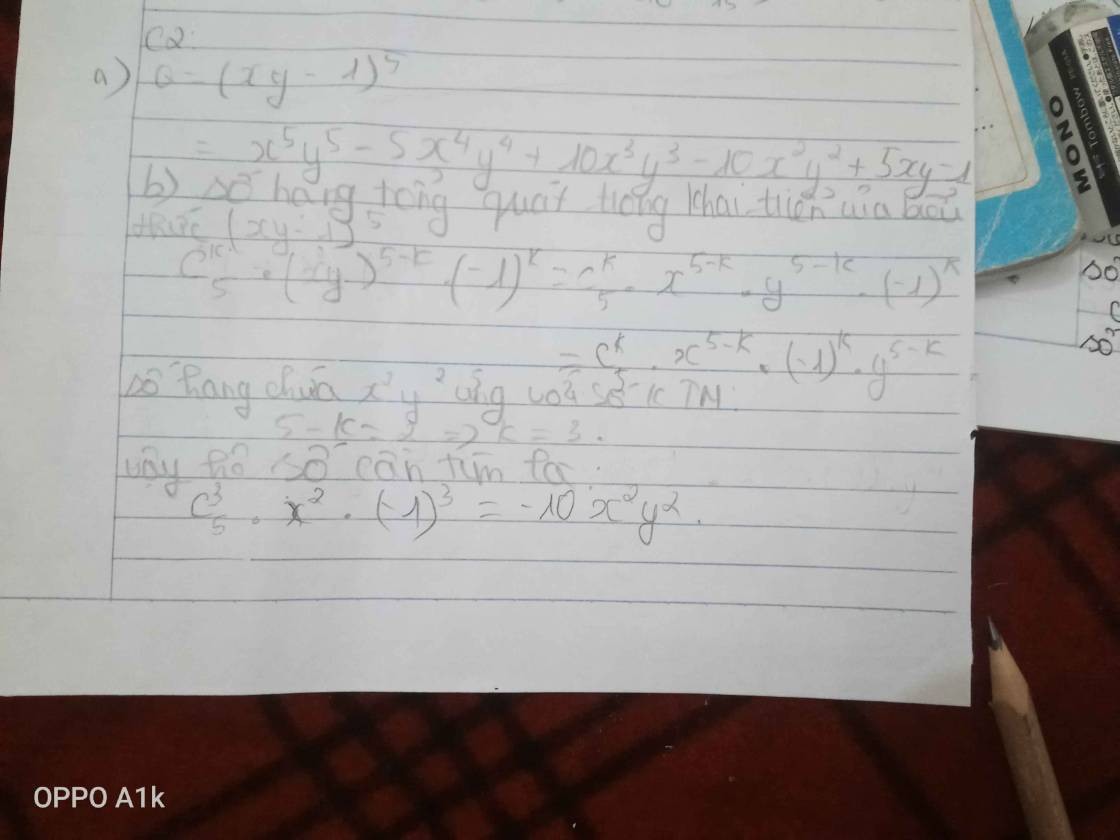Khai triển (a+b-c)2
TH
Những câu hỏi liên quan
Khai triển các biểu thức sau:a) A
(
a
+
b
+
c
)
2
;
b) B
(
a
–
b
–...
Đọc tiếp
Khai triển các biểu thức sau:
a) A = ( a + b + c ) 2 ; b) B = ( a – b – c ) 2 .
a) Sử dụng công thức bình phương của tổng với số hạng thứ nhất là a + b và số hạng thứ hai là c.
Biến đổi thu được A = a 2 + b 2 + c 2 + 2ab + 2bc + 2 ac;
b) a 2 + b 2 + c 2 - 2ab + 2bc - 2 ac.
Đúng 0
Bình luận (0)
Khai triển các biểu thức:
a) (a-b+c)2 b) (a+2b-c)2
c) (2a-b-c)2
a, \(\left(a-b+c\right)^2=a^2+b^2+c^2-2ab-2bc+2ca\)
Đúng 2
Bình luận (0)
b, \(\left(a+2b-c\right)^2=a^2+4b^2+c^2+4ab-4bc-2ca\)
Đúng 1
Bình luận (0)
c, \(\left(2a-b-c\right)^2=4a^2+b^2+c^2-4ab+2bc-4ca\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
8. Trong khai triển (8a^2 - 1/2b)^6 hệ số của số hạng chứa a^9.b^3 là?
9. Trong khai triển ( x + 8/x^2)^9 số hạng ko chứa x là?
A. 4308
B. 86016
C. 84
D. 43008
Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)
Đúng 1
Bình luận (0)
Khai triển các biểu thức sau:a) C
(
a
–
c
+
b
)
2
; b) D
(
x
+
1
–...
Đọc tiếp
Khai triển các biểu thức sau:
a) C = ( a – c + b ) 2 ; b) D = ( x + 1 – 2 y ) 2 .
a) a 2 + b 2 + c 2 + 2ab - 2bc - 2 ac.
b) 1 – 2x + x 2 .
Đúng 0
Bình luận (0)
a) Xét công thức khai triển {left( {a + b} right)^2} {a^3} + 3{a^2}b + 3a{b^2} + {b^3}i) Liệt kê các số hạng của khai triển trênii) Liệt kê các hệ số của khai triển trêniii) Tính giá trị của C_3^0,C_3^1,C_3^2,C_3^3 (có thể sử dụng máy tính) rồi so sánh với các hệ số trên. Có nhận xét gì?b) Hoàn thành biến đổi sau đây để tìm công thức khai triển của {left( {a + b} right)^4}{left( {a + b} right)^4} left( {a + b} right){left( {a + b} right)^3} ? ?{a^4} + ?{a^3}b + ?{a^2}{b^2} + ?a{b^3} + ?{b^4...
Đọc tiếp
a) Xét công thức khai triển \({\left( {a + b} \right)^2} = {a^3} + 3{a^2}b + 3a{b^2} + {b^3}\)
i) Liệt kê các số hạng của khai triển trên
ii) Liệt kê các hệ số của khai triển trên
iii) Tính giá trị của \(C_3^0,C_3^1,C_3^2,C_3^3\) (có thể sử dụng máy tính) rồi so sánh với các hệ số trên. Có nhận xét gì?
b) Hoàn thành biến đổi sau đây để tìm công thức khai triển của \({\left( {a + b} \right)^4}\)
\({\left( {a + b} \right)^4} = \left( {a + b} \right){\left( {a + b} \right)^3} = ? = ?{a^4} + ?{a^3}b + ?{a^2}{b^2} + ?a{b^3} + ?{b^4}\)
Tính giá trị của \(C_4^0,C_4^1,C_4^2,C_4^3,C_4^4\) để viết lại công thức khai triển trên
c) Từ kết quả của câu a) và b), hãy dự đoán công thức khai triển của \({\left( {a + b} \right)^5}\). Tính toán để kiểm tra dự đoán đó.
a)
i) Các số hạng của khai triển trên là: \({a^3},3{a^2}b,3a{b^2},{b^3}\)
ii) Các hệ số của khai triển trên là: \(1;3;3;1\)
iii) Tính các giá trị \(C_3^0,C_3^1,C_3^2,C_3^3\) ta được
\(C_3^0 = 1,C_3^1 = 3,C_3^2 = 3,C_3^3 = 1\)
Các giá trị của \(C_3^0,C_3^1,C_3^2,C_3^3\) bằng với các hệ số của khai triển đã cho
b)
\(\begin{array}{l}{\left( {a + b} \right)^4} = \left( {a + b} \right){\left( {a + b} \right)^3} = \left( {a + b} \right)\left( {{a^3} + 3{a^2}b + 3a{b^2} + {b^3}} \right)\\ = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\end{array}\)
Tính giá trị của \(C_4^0,C_4^1,C_4^2,C_4^3,C_4^4\) ta được
\(C_4^0 = 1,C_4^1 = 4,C_4^2 = 6,C_4^3 = 4,C_4^4 = 1\)
Vậy ta được khai triển là:
\({\left( {a + b} \right)^4} = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}\)
c)
Dự đoán công thức \({\left( {a + b} \right)^5} = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\)
Tính lại ta có
\(\begin{array}{l}{\left( {a + b} \right)^5} = {\left( {a + b} \right)^2}{\left( {a + b} \right)^3} = \left( {{a^2} + 2ab + {b^2}} \right)\left( {{a^3} + 3{a^2}b + 3a{b^2} + {b^3}} \right)\\ = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}\end{array}\)
Vậy công thức dự đoán là chính xác.
Đúng 0
Bình luận (0)
Khai triển các hằng đẳng thức
a. (a+b+c)^2
b. (a-b-c)^2
a) \((a+b+c)^2\) \(= a^2 + b^2 +c ^2 +2ab+2bc+2ca\)
b) \((a-b-c)^2 = a^2 + b^2 +c^2 - 2ab + 2bc -2ca\)
học tốt !
Đúng 0
Bình luận (0)
Khai triển :
a ) ( a - b + c )2
b ) ( a - b - c )2
a) ( a - b + c ) 2 = a2 + b2 + c2 + 2ab - 2ac - 2bc
b ) ( a - b - c )2 = a² + b² + c² - 2ab + 2bc - 2ca
Đúng 0
Bình luận (0)
Giải
a/\(\left(a-b+c\right)^2=a^2+b^2+c^2+2ab-2ac-2bc\)
b/\(\left(a-b-c\right)^2=a^2+b^2+c^2-2ab+2bc-2ca\)
Đúng 0
Bình luận (0)
Bài 1: Khai triển các hằng đẳng thức sau:a, (3x-5y)2b, (2x+7y)2c, 4x2-49d, (2x+3)3e, (2x-5)3f, (2x+3y)3g, (3x-2y)3Bài 2: Khai triển các hằng đẳng thức sau:a, (a+b+c)2b, (a-b+c)2c, (a+b-c)2d, (a-b-c)2Bài 3: Điền đơn thức thích hợp vào ô trống:a, 8x3+❏+❏+27y3(❏+❏)3b, 8x3+12x2.y+❏+❏(❏+❏)3c, x3-❏+❏-❏(❏-2y)3Bài 4: So sánh:a, 2003.2005 và 20042b, 716-1 và 8 ( 78+11) (74+1) (72+1) Bài 5: Đưa về hiệu hai bình:a, (2x-5) (2x+5)b, (3x-5y) (3x+5y)c, (3x+7y) (3x-7y)d, (2x-1.2x+1)Mọi người giúp mik giải gấp b...
Đọc tiếp
Bài 1: Khai triển các hằng đẳng thức sau:
a, (3x-5y)2
b, (2x+7y)2
c, 4x2-49
d, (2x+3)3
e, (2x-5)3
f, (2x+3y)3
g, (3x-2y)3
Bài 2: Khai triển các hằng đẳng thức sau:
a, (a+b+c)2
b, (a-b+c)2
c, (a+b-c)2
d, (a-b-c)2
Bài 3: Điền đơn thức thích hợp vào ô trống:
a, 8x3+❏+❏+27y3=(❏+❏)3
b, 8x3+12x2.y+❏+❏=(❏+❏)3
c, x3-❏+❏-❏=(❏-2y)3
Bài 4: So sánh:
a, 2003.2005 và 20042
b, 716-1 và 8 ( 78+11) (74+1) (72+1)
Bài 5: Đưa về hiệu hai bình:
a, (2x-5) (2x+5)
b, (3x-5y) (3x+5y)
c, (3x+7y) (3x-7y)
d, (2x-1.2x+1)
Mọi người giúp mik giải gấp bài này nha. Cảm ơn nhiều ạ
5:
a: (2x-5)(2x+5)=4x^2-25
b: (3x-5y)(3x+5y)=9x^2-25y^2
c: (3x+7y)(3x-7y)=9x^2-49y^2
d: (2x-1)(2x+1)=4x^2-1
4:
a: 2003*2005=(2004-1)(2004+1)=2004^2-1<2004^2
b: 8(7^2+1)(7^4+1)(7^8+1)
=1/6*(7-1)(7+1)(7^2+1)(7^4+1)(7^8+1)
=1/6(7^2-1)(7^2+1)(7^4+1)(7^8+1)
=1/6(7^16-1)<7^16-1
Đúng 3
Bình luận (0)
5:
a: (2x-5)(2x+5)=4x^2-25
b: (3x-5y)(3x+5y)=9x^2-25y^2
c: (3x+7y)(3x-7y)=9x^2-49y^2
d: (2x-1)(2x+1)=4x^2-1
mik chỉ biết bài 5 thôi !
Đúng 1
Bình luận (0)
Câu 2. (2 điểm) Cho biểu thức $Q=(x y-1)^5$.
a) Viết khai triển biểu thức $Q$ bằng nhị thức Newton.
b) Tìm số hạng có chứa $x^2 y^2$ trong khai triển trên.