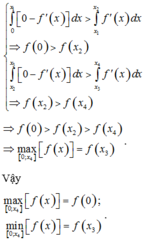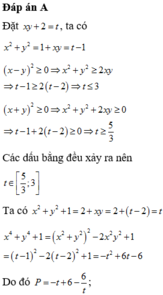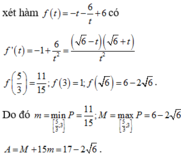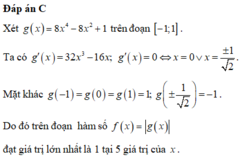Giá trị lớn nhất của D=20160-x2-x4 là
PH
Những câu hỏi liên quan
Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f
x
x
4
−
x
2
A. -2 B. 4 C. 2 D. 0
Đọc tiếp
Tìm tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x = x 4 − x 2
A. -2
B. 4
C. 2
D. 0
Tìm giá trị lớn nhất của biểu thức A=x2/x4+x2+1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau: y = x 4 + x 2 trên khoảng (− ∞ ;+ ∞ )
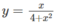 trên khoảng (−
∞
;+
∞
);
trên khoảng (−
∞
;+
∞
);
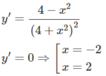
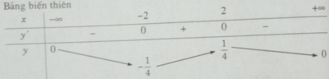
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4
Đúng 0
Bình luận (0)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - x 4 + x 2 - 1 trên đoạn [-2;1]. Tính M + m.
A. 0.
B. -9.
C. -10.
D. -1.
Chọn B.
Ta có: ![]() cho y' = 0
cho y' = 0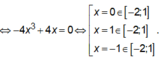
Ta có: ![]()
Suy ra ![]()
![]()
Vậy M + m = -9
Đúng 0
Bình luận (0)
Cho các số thực
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
0
x
1
x
2
x
3
x
4
và hàm số yf(x). Biết hàm số yf’(x) có đồ thị như hình vẽ. Gọi M và m lần...
Đọc tiếp
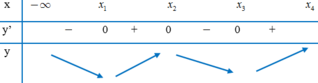
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y=f(x). Biết hàm số y=f’(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
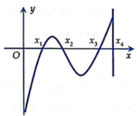
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Cho các số thực
x
1
,
x
2
,
x
3
,
x
4
thỏa mãn
0
x
1
x
2
x
3
x
4
và hàm số
y
f
x
. B...
Đọc tiếp
Cho các số thực x 1 , x 2 , x 3 , x 4 thỏa mãn 0 < x 1 < x 2 < x 3 < x 4 và hàm số y = f x . Biết hàm số y = f ' x có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn 0 ; x 4 . Đáp áp nào sau đây đúng?
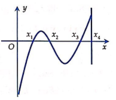
A. M + m = f 0 + f x 3 .
B. M + m = f x 3 + f x 4 .
C. M + m = f x 1 + f x 2 .
D. M + m = f 0 + f x 1 .
Đáp án A
Dựa vào đồ thị hàm số y = f ' x , ta có nhận xét:
Hàm số y = f ' x đổi dấu từ – sang + khi qua x = x 1 .
Hàm số y = f ' x đổi dấu từ + sang – khi qua x = x 2 .
Hàm số y = f ' x đổi dấu từ – sang + khi qua x = x 3 .
Từ đó ta có bảng biến thiên của hàm số y = f x trên đoạn 0 ; x 4 như sau:
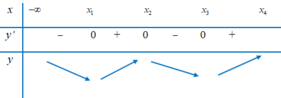
Sử dụng bảng biến thiên ta tìm được max 0 ; x 4 [ f x = max f 0 , f x 2 , f x 4 min 0 ; x 4 f x = min f x 1 , f x 3 .
Quan sát đồ thị, dùng phương pháp tích phân để tính diện tích, ta có:
∫ x 1 x 2 f ' x d x < ∫ x 2 x 3 0 − f ' x d x ⇒ f x 3 < f x 1 ⇒ min 0 ; x 4 f x = f x 3
Tương tự, ta có
∫ 0 x 1 0 − f ' x d x > ∫ x 1 x 2 f ' x d x ⇒ f 0 > f x 2 ∫ x 2 x 3 0 − f ' x d x > ∫ x 3 x 4 f ' x d x ⇒ f x 2 > f x 4
⇒ f 0 > f x 2 > f x 4 ⇒ max 0 ; x 4 f x = f x 3
Vậy max 0 ; x 4 f x = f 0 ; min 0 ; x 4 f x = f x 3
Đúng 0
Bình luận (0)
Cho x, y là những số thực thỏa mãn
x
2
–
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x...
Đọc tiếp
Cho x, y là những số thực thỏa mãn x 2 – x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15 m là
A. A = 17 - 2 6
B. A = 17 - 6
C. A = 17 + 6
D. A = 17 + 2 6
Cho x,y là những số thực thỏa mãn
x
2
-
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x
2
+
y...
Đọc tiếp
Cho x,y là những số thực thỏa mãn x 2 - x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15m là
A. A = 17 - 2 6
B. A = 17 + 6
C. A = 17 + 2 6
D. A = 17 - 6
cho hai số x,y thỏa mãn x2 + y2 =1 + xy , gọi M và m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của P = x4 + y4 -x2y2 , tính tích Mm
\(x^2+y^2=1+xy\Rightarrow x^2+y^2-xy=1\)
Ta có: \(1+xy=x^2+y^2\ge2xy\Rightarrow xy\le1\)
\(1+xy=x^2+y^2\ge-2xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(P=\left(x^2+y^2\right)^2-x^2y^2-2x^2y^2=\left(x^2+y^2-xy\right)\left(x^2+y^2+xy\right)-2x^2y^2\)
\(=x^2+y^2+xy-2x^2y^2=-2x^2y^2+2xy+1\)
Đặt \(a=xy\Rightarrow P=f\left(a\right)=-2a^2+2a+1\)
Xét hàm \(f\left(a\right)=-2a^2+2a+1\) trên \(\left[-\dfrac{1}{3};1\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{2}\in\left[-\dfrac{1}{3};1\right]\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow M=\dfrac{3}{2}\) ; \(m=\dfrac{1}{9}\) \(\Rightarrow Mm=\dfrac{1}{6}\)
Đúng 4
Bình luận (0)
Giá trị lớn nhất của hàm số y = x 4 + x 2 - 2 trên đoạn [-1;2] bằng
A. 18
B. 0
C. -2
D. 20