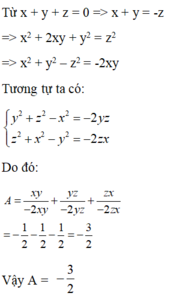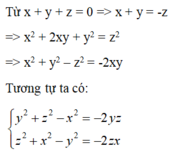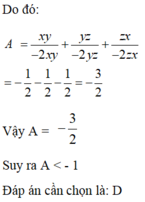Cho ba số x,y,z thỏa mãn x2+y2+z2>0. Chứng minh rằng: x2+19y2+6z2-8xy-4xz+12yz>0
NP
Những câu hỏi liên quan
Cho ba số x,y,z thỏa mãn x2+y2+z2>0. Chứng minh rằng: x2+19y2+6z2-8xy-4xz+12yz>0
phân tích thành (a-b-c)2
rồi tách tiếp con còn lại thành HĐT
tớ làm đến bước x=y=z r tịt lun
Đúng 0
Bình luận (0)
Cho ba số x, y và z thỏa mãn x + y + z = 0. Chứng minh rằng
2(x5 + y5 + z5) = 5xyz(x2 + y2 + z2).
Lời giải:
$x^5+y^5+z^5=(x^2+y^2+z^2)(x^3+y^3+z^3)-[x^2(y^3+z^3)+y^2(x^3+z^3)+z^2(x^3+y^3)]$
Mà:
$x^3+y^3+z^3=(x+y)^3-3xy(x+y)+z^3$
$=(-z)^3-3xy(-z)+z^3=3xyz$
Và:
\(x^2(y^3+z^3)+y^2(x^3+z^3)+z^2(x^3+y^3)\)
\(=x^2y^2(x+y)+y^2z^2(y+z)+z^2x^2(z+x)=-x^2y^2z-y^2z^2x-x^2y^2z\)
\(=-xyz(xy+yz+xz)=-xyz[\frac{(x+y+z)^2-(x^2+y^2+z^2)}{2}]=\frac{xyz(x^2+y^2+z^2)}{2}\)
Do đó: \(x^5+y^5+z^5=3xyz(x^2+y^2+z^2)-\frac{xyz(x^2+y^2+z^2)}{2}=\frac{5xyz(x^2+y^2+z^2)}{2}\)
\(\Rightarrow 2(x^5+y^5+z^5)=5xyz(x^2+y^2+z^2)\)
Ta có đpcm.
Đúng 1
Bình luận (0)
cho xyz khác 0 và thỏa mãn x2=y.z,y2=x.z,z2 =x.y. chứng minh x =y=z
\(x^2=y.z\Rightarrow x^3=x.y.z\\ y^2=x.z\Rightarrow y^3=x.y.z\\ z^2=x.y\Rightarrow z^3=x.y.z\\ \Rightarrow x^3=y^3=z^3\\ \Rightarrow x=y=z\)
Đúng 1
Bình luận (0)
Cho x,y,z thỏa mãn x2+y2+z2>0.CMR: x2+19y2+6z2-8xy-4xz+12yz>0
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Tính giá trị biểu thức: A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2
+...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Tính giá trị biểu thức: A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A = 1 2
B. A = - 1 2
C. A = - 3 2
D. A = 3 2
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Chọn câu đúng về biểu thức
A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Chọn câu đúng về biểu thức A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A < -2
B.0 < A < 1
C. A > 0
D. A < -1
Cho các số thực x, y, z, a, b, c thỏa mãn: x+y+z=1; x2+y2+z2=1 và a/x=b/y=c/z.
Chứng minh rằng: ab + bc + ca =0
Lời giải:
Đặt $\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=t$
$\Rightarrow a=xt; b=yt; c=zt$. Ta có:
$a+b+c=xt+yt+zt=t(x+y+z)=t$
$a^2+b^2+c^2=t^2(x^2+y^2+z^2)=t^2$
$ab+bc+ac=\frac{(a+b+c)^2-(a^2+b^2+c^2)}{2}=\frac{t^2-t^2}{2}=0$
Ta có đpcm.
Đúng 1
Bình luận (0)
Cho x, y, z ≠0 và (y2+z2−x2)/2yz +(z2+x2−y2)/2xz +(x2+y2−z2)/2xy =1. Chứng minh rằng trong ba phân thức đã cho có một phân thức bằng 1 và một phân thức bằng -1.
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) (ax + by + cz)2 thì a/x b/y c/z.
Đọc tiếp
Bài 3 Chứng minh rằng với a, b, c, x, y, z (trong đó xyz 6= 0) thỏa mãn (a2 + b2 + c2)(x2 + y2 + z2) = (ax + by + cz)2
thì a/x =b/y =c/z.
Cho x,y,z là số dương thoa mãn x2+y2-z2>0 Chứng minh x+y-z>0