Tứ giác ABCD có góc A = 65 độ, góc B = 117 độ, góc C = 71 độ. Tính góc D
H24
Những câu hỏi liên quan
Cho tứ giác ABCD có góc A = 65 độ, góc B = 117 độ, góc C = 71 độ. Tính số đo của góc D =?
a 126 độ
b 63 độ
c 119 độ
d 107 độ
Xem thêm câu trả lời
tứ giác ABCD có góc A=65 độ , góc B=117 độ , góc C = 71 độ . Tinh số đo góc ngoài tại đỉnh D
Xét hình tứ giác ABCD có:
\(A+B+C+D=360^0\) (đ/l.....)
=>\(D=360^0-\left(A+B+C\right)=360^0-\left(65^0+117^0+71^0\right)=107^0\)
=>số đo góc ngoài ở đỉnh D là : 1800-1070=730
Đúng 0
Bình luận (0)
Xét hình tứ giác ABCD :
A+B+C+D=360
=>D=1070
=>số đo góc ngoài ở đỉnh D là : 1800-1070=730
Đúng 3
Bình luận (0)
tứ giác ABCD có góc A =65 độ;góc B=117 độ;góc C=71 độ.Tính số đo góc ngoài đỉnh C
mik đang cần gáp bài này mn giúp mik với
Đúng 0
Bình luận (0)
Số đo góc ngoài đỉnh C là:
\(180^0-71^0=109^0\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có A=65 độ, B=117 độ, C=68 độ. Tính số đo góc ngoài tại đỉnh D
Số đo góc D là: 360o - 65o - 117o - 68o = 110o
Số đo góc ngoài đỉnh D: 180o - 110o = 70o
Đúng 1
Bình luận (0)
Số đo góc ngoài tại đỉnh D là:
\(180^0-\left(360^0-65^0-117^0-68^0\right)=70^0\)
Đúng 1
Bình luận (0)
1. cho tứ giác ABCD biết góc A : góc B : góc c ; góc D 1:2:3:4 tính các góc của tứ giác2. chó tứ giác ABCD có góc A 105 độ: góc B 130 độ, góc C-góc D 25 độ. Tính góc C, góc D3. Cho tứ giác ABCD có góc A 57 độ, C 110 độ, D 75 độ. Tính góc ngoài tại B4. Chứng minh rằng: Biết 1 tứ giác tổng 2 đường chéo lớn hơn nửa chu vi của tứ giác 5. Cho tứ giác ABCD có góc B+gócD 180 độ, AC là tia phân giác góc A. Chứng minh cạnh CB cạnh CD
Đọc tiếp
1. cho tứ giác ABCD biết góc A : góc B : góc c ; góc D = 1:2:3:4 tính các góc của tứ giác
2. chó tứ giác ABCD có góc A =105 độ: góc B = 130 độ, góc C-góc D = 25 độ. Tính góc C, góc D
3. Cho tứ giác ABCD có góc A = 57 độ, C= 110 độ, D= 75 độ. Tính góc ngoài tại B
4. Chứng minh rằng: Biết 1 tứ giác tổng 2 đường chéo lớn hơn nửa chu vi của tứ giác
5. Cho tứ giác ABCD có góc B+gócD= 180 độ, AC là tia phân giác góc A. Chứng minh cạnh CB = cạnh CD
1: Đặt góc A=a; góc B=b; góc C=c; góc D=d
Theo đề, ta có: a/1=b/2=c/3=d/4 và a+b+c+d=360
Áp dụng tính chất của DTSBN, ta được:
a/1=b/2=c/3=d/4=(a+b+c+d)/(1+2+3+4)=360/10=36
=>a=36; b=72; c=108; d=144
2:
góc C+góc D=360-130-105=230-105=125
góc C-góc D=25 độ
=>góc C=(125+25)/2=75 độ và góc D=75-25=50 độ
3:
góc B=360-57-110-75=118 độ
số đo góc ngoài tại B là:
180-118=62 độ
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc ngoài tại điểm A =65 độ, góc ngoài tại điểm B=100 độ, góc ngoài ở điểm C= 60 độ . Tính góc ngoài ở điểm D
Ta có tổng các góc trong tứ giác là:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Mà các góc ngoài của các đỉnh của được tính tương tự:
Tổng các góc ngoài của các đỉnh là:
\(\widehat{A_{\text{ngoài}}}+\widehat{B_{\text{ngoài}}}+\widehat{C_{\text{ngoài}}}+\widehat{D_{\text{ngoài}}}=360^o\)
\(\Rightarrow\widehat{D_{\text{ngoài}}}=360^o-\left(65+100+60\right)=135^o\)
Đúng 1
Bình luận (0)
Số đo góc ngoài tại điểm D là:
360-65-100-60=135 độ
Đúng 1
Bình luận (0)
Cho tứ giác ABCD
AB//CD, Góc C = 65 độ, góc D = 95 độ, tính góc A và góc B
AB // CD
=> A + D = 1800 (2 góc trong cùng phía)
A + 950 = 1800
A = 1800 - 950
A = 850
AB // CD
=> B + C = 1800 (2 góc trong cùng phía)
B + 650 = 1800
B = 1800 - 650
B = 1150
Đúng 0
Bình luận (0)
Ta gọi tứ giác ABCD có AB=AD,CB=CD là hình “cái diều”.
a)CMinh rằng AC là đường trung trực của BD.
b)Tính góc B,góc D biết rằng góc A=100 độ,góc C=60 độ.
c)Giả sử cho góc ABC=117 độ,góc BAD bằng 2 lần góc BCD.Tính các góc của tứ giác ABCD.
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
nên ∆ ABC = ∆ADC (c.c.c)
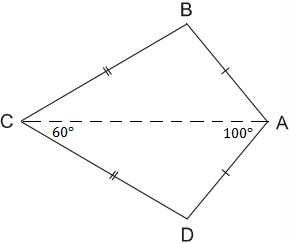
Suy ra: ⇒ˆB=ˆD
Ta có ˆB+ˆD=3600–(100+60)=200
Do đó ˆB=ˆD=1000
Đúng 1
Bình luận (0)
mban trl giúp mình câu C luôn nha ạ😭
Đúng 0
Bình luận (0)
Mình làm hơi tắt
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Mà \(\widehat{A}=2\times\widehat{C}\left(gt\right)\)
\(\widehat{B}=\widehat{D}=117^o\)theo câu b)
\(\Rightarrow2\times\widehat{C}+117^o+\widehat{C}+117^o=360^o\)
\(\Rightarrow3\times\widehat{C}=360^o-117^o-117^o=126^o\)
\(\Rightarrow\widehat{C}=\frac{126^o}{3}=42^o\)
\(\Rightarrow\widehat{A}=2\times\widehat{C}=2\times42^o=84^o\)
Vậy \(\widehat{A}=84^o;\widehat{B}=117^o;\widehat{C}=42^o;\widehat{D}=117^o\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tứ giác ABCD có góc A-B = 15 độ , góc C+D = 175 độ , góc A+D=210 độ. Tính số đo các góc của tứ giác ABCD
Bài 3: Cho tứ giác ABCD có AB//CD và góc D =60 độ
a) Tính số đo góc A?
b) Biết góc B phần góc D = 4/5. Tính góc B, góc C
Bài 4: Cho tứ giác ABCD, góc A - góc B = 40 độ. Các tia phân giác của góc C, góc D cắt nhau tại O. Cho biết góc COD= 110 độ. Chứng minh rằng AB vuông góc với BC
Nhờ các bạn hướng dẫn mình hai bài này
a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.
Vì AB//CD, ta có góc ACD = góc BAD.
Vậy số đo góc A là 120 độ.
b) Gọi góc BCD là x độ.
Theo giả thiết, góc B phần góc D = 4/5, ta có:
góc B = (4/5) * góc D
= (4/5) * 60
= 48 độ.
Vì AB//CD, ta có góc BCD = góc BAD.
Vậy góc BAD = góc BCD = x độ.
Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.
Ta có: góc A + góc B + góc C + góc D = 360 độ.
Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:
120 + 48 + góc C + 60 = 360
góc C = 360 - 120 - 48 - 60 = 132 độ.
Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.
* Ib = bài 4
Đúng 0
Bình luận (0)





