Gọi M là trung điểm của cạnh BC của tam giác ABC ; trên cạnh AB lấy hai điểm D và E sao cho AD=DE=EB
a) chứng minh rằng ME//CD
b)chứng minh:Đoạn thẳng CD cắt đoạn thẳng AM ở trung điểm I
c) chứng minh: CI=3DI
a: Xét ΔNAB có
NM vừa là đường cao, vừa là trung tuyến
nên ΔBAN cân tại N
b: Xét ΔBAC có
M là trung điểm của BA
MN//AC
Do đó: N là trung điểm của BC
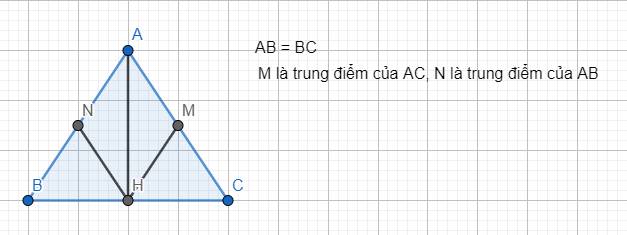
cho tam giác ABC cân tại A. Gọi H là trung điểm của BC
a) Chứng minh tam giác ABH=tam giác ACH
b)Gọi M là trung điểm của cạnh AC và N là trung điểm của cạnh AB. Chứng minh HN=HM
a, Xét tam giác \(\Delta ABH\) và \(\Delta ACH\) có :
\(HB=HC\left(gt\right)\)
\(\widehat{B}=\widehat{C}\left(gt\right)\)
\(AB=AC\left(gt\right)\)
= > \(\Delta ABH=\Delta ACH\left(c-g-c\right)\)
b, M là trung điểm của cạnh AC = > MA = 1/2 AC ( 1 )
N là trung điểm của cạnh AB = > NA = 1/2 AB ( 2 )
Từ ( 1 ) , ( 2 ) = > MA = NA ( Do AB = AC )
Mà tam giác ABH = tam giác ACH ( câu a, )
= > \(\widehat{BAH}=\widehat{CAH}\) ( 2 góc tương ứng )
Xét \(\Delta ANH\) và \(\Delta AMH\) có :
\(AN=AM\left(cmt\right)\)
\(\widehat{BAH}=\widehat{CAH}\left(cmt\right)\)
AH chung
= > \(\Delta ANH=\Delta AMH\left(c-g-c\right)\)
= > HN = HM ( 2 cạnh tương ứng )
a) Xét hai tam giác ABH và ACH ta có:
- AB = AC (vì ABC là tam giác cân)
- HB = HC (vì H là trung điểm của BC)
- \(\widehat{B}=\widehat{C}\) (vì ABC là tam giác cân)
Vậy \(\Delta ABH=\Delta ACH\) (c.g.c)
b) Xét hai tam giác NBH và MCH ta có:
- NB = MC (vì AB = AC, M là trung điểm của AC và N là trung điểm của AB)
- HB = HC (đã chứng minh trên)
- \(\widehat{B}=\widehat{C}\) (đã chứng minh trên)
Suy ra \(\Delta NBH=\Delta MCH\) (c.g.c)
Khi đó HN = HM (vì hai cạnh tương ứng)
cho hình tam giác ABC . gọi M là trung điểm của cạnh BC , gọi N là trung điểm của cạnh AB , biết diện tích hình tam giác AMN = 6 cm2 . tính diện tích hình tam giác ABC ? giúp mình nha !!!!!!!
Cho hình tam giác ABC
Gọi M là trung điểm của cạnh BC , gọi N là trung điểm của cạnh ẠB . Biết diện tích hình tam giác ANM là 6m2 . Tính diện tích hình tam giác ABC ???
( giải cẩn thận nha !!!)
Thế thì bạn giải giùm đi mình cũng ko biết làm, mai phải nộp cho thầy kiểm tra rồi
Sabm=Sabm x 2(Vì chung chiều cao hạ từ đỉnh M
,đáy AB=AN x 2)
Diên tích hình tam giác ABM là:
6x2=12(cm2)
Diện tích hình tam giác ABC là:
12x2=24(cm2)
Đ/S:24cm2
Cho hình tam giác ABC.Gọi M là trung điểm của cạnh BC,gọi N là trung điểm của cạnh AB.Biết diện tích hình tam giác ANM bằng 6 cm vuông.Tính diện tích hình tam giác ABC
Ta có diện tích ANM = NMB vì có hai cạnh đáy là NB=NA. Đều có chiều cao hạ từ đỉnh M.
Diện tích tam giác BAM là
Ta có diện tích ANM = NMB vì có hai cạnh đáy là NB=NA. Đều có chiều cao hạ từ đỉnh M.
Diện tích tam giác BAM là
6+6 =12 (cm2)
Diện tích tam giác ABM = AMC vì có đáy BM = Mc. Đều có chiều cao hạ từ đỉnh A nên diện tich ABC là :
12+12=24 (cm2)
Đ/S : 24 cm2
ĐÚNG là bằng 24cm2 đó, mấy bạn lớp mình cũng làm bằng chừng đó
Bài 1: Cho tam giác ABC, gọi M,N lần lượt là trung điểm của AB, AC.
a)Chứng minh MN // BC
b)Gọi D là điểm bất kỳ thuộc cạnh BC ( D khác B,C), AD cắt MN tại I. Chứng
minh I là trung điểm của AD.
Bài 2: Cho tam giác ABC cân tại A, M là trung điểm của BC. Kẻ Mx// AC cắt AB tại E, kẻ My// AB cắt AC tại F. Chứng minh rằng:
1)E,F là trung điểm của AB, AC
2) FE = 1/2 BC
3) ME=MF, AE=FA
Bài 1 : a) M là trung điểm AB
N là trung điểm AC
suy ra : MN là Đường trung bình của tam giác ABC
suy ra : MN // BC ; MN = BC/2
b) Ta có : MN // BC và M là trung điểm AB
Mà AD cắt MN tại I nên từ đó suy ra : I là trung điểm của cạnh AD
em chỉ giải được bài 1 thôi nên thông cảm ạ
cho tam giác ABC gọi M là trung điểm của cạnh BC , N là trung điểm của AC . Các đường trung trực của cạnh BCvà AC cắt nhau tại O . H là trực tâm , G là trọng tâm của tam giác.