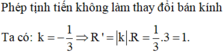Cho đường tròn (C) tâm O, bán kính R=1. Biết (C') là ảnh của (C) qua phép tịnh tiến vectơ v=(-2;5). Điểm M thuộc (C') sao cho OM ngắn nhất. Tìm độ dài OM khi đó?
NT
Những câu hỏi liên quan
Trong mp Oxy, cho đường tròn (C) có tâm I(2;–6) , bán kính R 3. Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ
u
→
−
4
;
0
A.
x
+
6
2
+
y
−
6
2...
Đọc tiếp
Trong mp Oxy, cho đường tròn (C) có tâm I(2;–6) , bán kính R = 3. Ảnh của đường tròn (C) qua phép tịnh tiến theo vectơ u → = − 4 ; 0
A. x + 6 2 + y − 6 2 = 9
B. x + 2 2 + y + 6 2 = 9
C. x − 6 2 + y + 6 2 = 9
D. x + 6 2 + y − 1 2 = 3
Đáp án B
T u → ( I ) = I ' − 2 ; − 6 , bán kính 3
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(1;−1) , bán kính R 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 1800và phép tịnh tiến theo vectơ
u
→
2
;
−
3
A.
x
+
1
2
+
y
+...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(1;−1) , bán kính R = 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 1800và phép tịnh tiến theo vectơ u → = 2 ; − 3
A. x + 1 2 + y + 2 2 = 9
B. x − 1 2 + y + 2 2 = 9
C. x + 1 2 + y + 2 2 = 36
D. x − 1 2 + y + 2 2 = 36
Đáp án B
Q ( O ; 180 o ) : I → I ' (–1;1) , bán kính 3
T u → ( I ) = I ' 1 ; − 2 bán kính 3
Phương trình đường tròn (C”): x − 1 2 + y + 2 2 = 9
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180
°
và phép vị tự tâm O tỉ số 2, phép tịnh tiến theo vectơ
u
→
1
;
2
A.
x
−
4
2
+
y...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I(0;−1) , bán kính R = 3. Ảnh của (C) qua việc thực hiện liên tiếp phép quay tâm O góc quay 180 ° và phép vị tự tâm O tỉ số 2, phép tịnh tiến theo vectơ u → 1 ; 2
A. x − 4 2 + y − 1 2 = 9
B. x − 1 2 + y − 4 2 = 9
C. x − 1 2 + y − 4 2 = 36
D. x − 4 2 + y − 1 2 = 36
Đáp án C
Q ( O ; 180 o ) : I → I ' (0;1) , bán kính 3
I ' ' = V O ; k ( I ' ) => I”(0;2), bán kính 6
T u → ( I " ) = I ' " 1 ; 4 , bán kính 6
Phương trình đường tròn (C”): ( x − 1 ) 2 + y − 4 2 = 36
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C):
x
-
2
2
+
y
+
1
2
9
Gọi (C’) là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số k
-
1
3...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x - 2 2 + y + 1 2 = 9 Gọi (C’) là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số k= - 1 3 và phép tịnh tiến theo vecto v → = ( 1 ; - 3 ) . Tìm bán kính R’ của đường tròn (C’).
A. 9
B. 3
C. 27
D. 1
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
:
x
−
2
2
+
y
+
1
2
9.
Gọi (C’) là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số
k
−
1
3...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C : x − 2 2 + y + 1 2 = 9. Gọi (C’) là ảnh của đường tròn (C) qua việc thực hiện liên tiếp phép vị tự tâm O, tỉ số k = − 1 3 và phép tịnh tiến theo v e c t o v → = 1 ; − 3 . Tìm bán kính R’ của đường tròn (C’).
A. R' = 9
B. R' = 3
C. R' = 27
D. R' = 1
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3;-2), bán kính 3.a. Viết phương trình của đường tròn đó.b. Viết phương trình ảnh của đường tròn (I;3) qua phép tịnh tiến theo vectơ v(-2 ;1).c. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng trục Ox.d. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng qua gốc tọa độ
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn tâm I(3;-2), bán kính 3.
a. Viết phương trình của đường tròn đó.
b. Viết phương trình ảnh của đường tròn (I;3) qua phép tịnh tiến theo vectơ v=(-2 ;1).
c. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng trục Ox.
d. Viết phương trình ảnh của đường tròn (I;3) qua phép đối xứng qua gốc tọa độ
a. Phương trình đường tròn : (x – 3)2 + (y + 2)2 = 9.
b. (I1; R1) là ảnh của (I; 3) qua phép tịnh tiến theo vec tơ v.
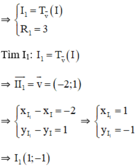
⇒ Phương trình đường tròn cần tìm: (x – 1)2 + ( y + 1)2 = 9.
c. (I2; R2) là ảnh của (I; 3) qua phép đối xứng trục Ox
⇒ R2 = 3 và I2 = ĐOx(I)
Tìm I2: I2 = ĐOx(I) ⇒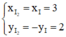 
⇒ I2(3; 2)
⇒ Phương trình đường tròn cần tìm: (x – 3)2 + (y – 2)2 = 9.
d. (I3; R3) là ảnh của (I; 3) qua phép đối xứng qua gốc O.
⇒ R3 = 3 và I3 = ĐO(I)
Tìm I3: I3 = ĐO(I) ⇒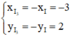 
⇒ Phương trình đường tròn cần tìm: (x + 3)2 +(y – 2)2 = 9.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho đường tròn
C
:
x
+
1
2
+
y
-
2
2
4
. Viết phương trình đường tròn ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số...
Đọc tiếp
Trong mặt phẳng Oxy, cho đường tròn
C : x + 1 2 + y - 2 2 = 4 . Viết phương trình đường tròn ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số k = 2 và phép tịnh tiến theo vectơ v = ( 1;2 ).
A. x - 3 2 + y - 6 2 = 16
B. x - 3 2 + y - 6 2 = 4
C. x - 1 2 + y - 2 2 = 16
D. x - 1 2 + y - 2 2 = 4
V 0 ; 2 : M x ; y → M ' x ' ; y ' ⇔ O M ' → = 2 O M ' → ⇔ x ' = 2 x y ' = 2 y
T v : M ' x ' ; y ' → M ' ' x ' ' ; y ' ' ⇔ x " = x ' + 1 y " = y ' + 2
Do đó phép đồng dạng F: M (x;y ) → M" ( x";y" ) có tọa độ thỏa mãn hệ thức
x = x ' 2 = x " - 1 2 y = y ' 2 = y " - 2 2
Do M ( x;y ) ∈ ℂ nên
x " - 1 2 - 1 2 + y " - 2 2 - 2 2 = 4 ⇔ x " - 3 2 + y " - 6 2 = 16
Vậy ảnh của (C) qua F là đường tròn có phương trình x - 3 2 + y - 6 2 = 16
Đáp án cần chọn là A
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho điểm M(3;5) , đường thẳng d:3x+2y-4=0 và đường tròn c:x^2+y^2-2x+4y-4=0
a. Tìm ảnh của điểm M và đường thẳng d qua phép tịnh tiến theo vectơ = (2;1)
b. Tìm ảnh của đường tròn (C) qua phép quay tâm O góc quay 90 độ (O là gốc tọa độ).
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
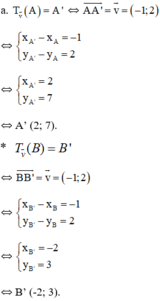
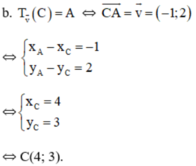
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Đúng 0
Bình luận (0)
Cho đường tròn (C) có tâm I(1;2) và bán kính
R
3
. Phép tịnh tiến theo vecto
v
→
2
;
0
biến (C) thành (C’) có phương trình là A.
x
−
3
2
+
y
−...
Đọc tiếp
Cho đường tròn (C) có tâm I(1;2) và bán kính R = 3 . Phép tịnh tiến theo vecto v → 2 ; 0 biến (C) thành (C’) có phương trình là
A. x − 3 2 + y − 2 2 = 9
B. x − 1 2 + y + 2 2 = 9
C. x + 3 2 + y + 2 2 = 9
D. x − 3 2 + y − 2 2 = 3
