1.Với  a = 2 ta có 2a + 1 = 5 không thích hợp

Với a   ≠ 2  do a là số nguyên tố nên a lẽ

Vậy 2a + 1 là lập phương của một số lẽ nghĩa là

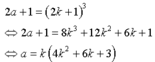
Từ đó k là ước của a. Do k là số nguyên tố nên k = 1 hoặc k = a

-Nếu k = 1 thì 2a + 1 = (2.1 + 1)³ suy ra a = 13 thớch hợp

-   Nếu a = k từ a = a(4a² + 6a + 3) do a là nguyên tố nên suy ra

 1 = 4a² + 6a + 3  không có số nguyên tố a nào thoả món phương trỡnh này  Vì vế phải luụn lớn hơn 1

Vậy a = 13

2.Giả sử  

13 và p là các số nguyên tố , mà n – 1 > 1 và n² + n + 1 > 1

Nên n – 1 = 13 hoặc  n – 1 = p

-    Với n – 1 =13 thì n = 14 khi đó 13p = n³ – 1 = 2743 suy ta p = 211 là số nguyên tố

- Với n – 1 = p thi n² + n + 1 = 13 suy ra n = 3 . Khi đó p = 2 là số nguyên tố

 Vậy  p = 2, p = 211 thì 13p + 1  là lập phương của một số tự nhiên

fffffffffffffffffffffffffffffffffffffffffffff

what the fuck

đag học ,tự nhiên vào phá 

kêu rằng :f f f f f f ...

a. a =1 

b . p = 22

xin lỗi tớ nhầm 

Đặt 2p + 1 = n³ với n là số tự nhiên 

Cách giải: phân tích ra thừa số 
Dùng tính chất : Số nguyên tố có 2 ước là 1 và chính nó. 

Giải: 

♣ Ta thấy p = 2 thì 2p + 1 = 5 không thỏa = n³ 

♣ Nếu p > 2 => p lẻ (Do Số nguyên tố chẵn duy nhất là 2 ) 
Mặt khác : 2p + 1 là 1 số lẻ => n³ là một số lẻ => n là một số lẻ 

=> 2p + 1 = (2k + 1)³ ( với n = 2k + 1 ) 
<=> 2p + 1 = 8k³ + 12k² + 6k + 1 
<=> p = k(4k² + 6k + 3) 

=> p chia hết cho k 
=> k là ước số của số nguyên tố p. 

Do p là số nguyên tố nên k = 1 hoặc k = p 

♫ Khi k = 1 
=> p = (4.1² + 6.1 + 3) = 13 (nhận) 

♫ Khi k = p 
=> (4k² + 6k + 3) = (4p² + 6p + 3) = 1 
Do p > 2 => (4p² + 6p + 3) > 2 > 1 
=> không có giá trị p nào thỏa. 

Đáp số : p = 13

2:

a: 7;49

b: 30;60;90;120

Do p là SNT nên \(p^4\) chỉ có các ước nguyên dương là \(1;p;p^2;p^3;p^4\)

\(\Rightarrow1+p+p^2+p^3+p^4=k^2\) với \(k\in N\)

\(\Rightarrow\left(2k\right)^2=4p^4+4p^3+4p^2+4p+4=\left(2p^2+p\right)^2+\left(3p^2+4p+4\right)>\left(2p^2+p\right)^2\)

Đồng thời: \(4p^4+4p^3+4p^2+4p+4=\left(2p^2+p+2\right)^2-5p^2< \left(2p^2+p+2\right)^2\)

\(\Rightarrow\left(2p^2+p\right)^2< \left(2k\right)^2< \left(2p^2+p+2\right)^2\)

\(\Rightarrow\left(2k\right)^2=\left(2p^2+p+1\right)^2\)

\(\Rightarrow4p^4+4p^3+4p^2+4p+4=\left(2p^2+p+1\right)^2\)

\(\Rightarrow p^2-2p-3=0\Rightarrow\left[{}\begin{matrix}p=-1\left(ktm\right)\\p=3\left(tm\right)\end{matrix}\right.\)