ai giúp mình câu này với ạ. mình cảm ơn
SS
Những câu hỏi liên quan
Ai làm giúp mình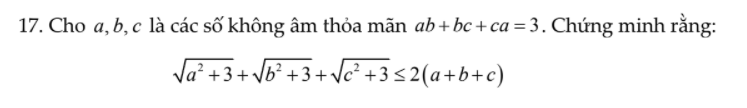 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.
\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)
Đúng 0
Bình luận (0)
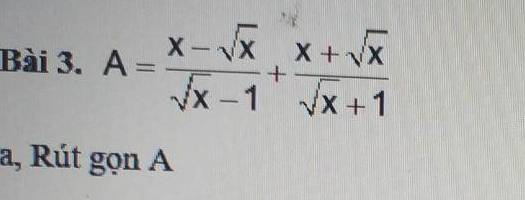
ai giải giúp mình câu này với ạ. mình cảm ơn
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}+\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}+\sqrt{x}=2\sqrt{x}\)
Đúng 1
Bình luận (0)
Ai làm giúp mình 2 câu này với ạ! Mình cảm ơn.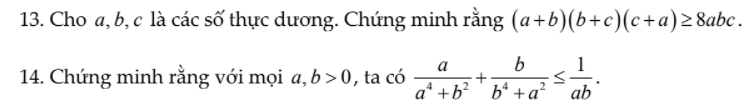
1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)
Đúng 1
Bình luận (0)
Ai giải thích giúp mình câu này với ạ, mình cảm ơn
TH1: thể 3 ở A, B, E
A-B-ddE- = 3.3.2.1.2 = 36
TH2: Thể 3 ở d
A-B-ddE- = 2.2.1.2 = 8
Tổng là 44
Đúng 1
Bình luận (3)
Ai giúp mình làm 3 câu này với ạ mình đang cần gấp. Cảm ơn mn nhiều ạ.
Ai giúp mình 2 câu 4 và 5 này với ạ! Mình cảm ơn nhiều!

Có ai đó giúp em/mình câu này với ạ e cảm ơn.
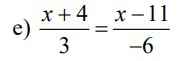
\(\dfrac{x+4}{3}=\dfrac{x-11}{-6}\)
\(\dfrac{2x+8}{6}=\dfrac{-x+11}{6}\)
\(\Leftrightarrow2x+8=-x+11\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\)
Đúng 3
Bình luận (0)
Nhân chéo ta được\(-6(x+4)=3(x-11)=>-6x-24=3x-33=>6x-3x-24+33=0=>3x+9=0=>3x=-9=>x=-3\)
Đúng 3
Bình luận (0)
Giúp mình câu này với ạ mình cảm ơn
Giúp mình câu này với ạ. Mình cảm ơn







