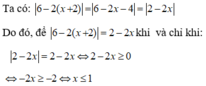Có tất cả bao nhiêu giá trị thảo mãn |x^2-2x|=x
NM
Những câu hỏi liên quan
Tất cả có bao nhiêu giá trị x thỏa mãn:
|x^2 - 2x|= x
giúp mik vs!!!!!!!!
Vì |x^2- 2x| >=0 suy ra x>=0
TH1 x^2-2x=x
suy ra x^2-3x=0
suy ra x=0 (TM) hoặc x=3(TM)
TH2 x^2-2x=-x
suy ra x^2-x=0
suy ra x=0(Tm) hoặc x=1 (tm)
Vậy có 3 giá trị x thỏa mãn là 0;1;3
NHỚ !!!!!!!!!!!
Đúng 0
Bình luận (0)
mơn bn Siêu Quậy nha!!!!!!!!!
Đúng 0
Bình luận (0)
tập hợp tất cả các giá trị của x thõa mãn
/2x-5/=x-1 có số phần tử là bao nhiêu
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình
8
x
.
2
1
-
x
2
≥
(
2
)
2
A. ...
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 ≥ ( 2 ) 2
A. 4
B. 5
C. 2
D. 3
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình
8
x
.
2
1
-
x
2
2
2
x
A. 4 B. 5 C. 2 D. 3
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 > 2 2 x
A. 4
B. 5
C. 2
D. 3
Ta có:
8 x . 2 1 - x 2 > 2 2 x ⇔ 2 3 x + 1 - x 2 > 2 x ⇔ 3 x + 1 - x 2 > x ⇔ x 2 - 2 x - 1 < 0 ⇔ 1 - 2 < x < 1 + 2
Mà x ∈ ℝ ⇒ x ∈ 1 ; 2 . Bất phương trình đã cho có 2 nghiệm nguyên dương.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình
8
x
.
2
1
-
x
2
2
2
x
A. 4 B. 5 C. 2 D. 3
Đọc tiếp
Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình 8 x . 2 1 - x 2 > 2 2 x
A. 4
B. 5
C. 2
D. 3
Có tất cả bao nhiêu giá trị của x thỏa mãn đồng thời hai điều kiện x + 1/3 là số nguyên và
log
1
3
5
-
x
log
1
3
3
-
x
? A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Có tất cả bao nhiêu giá trị của x thỏa mãn đồng thời hai điều kiện x + 1/3 là số nguyên và log 1 3 5 - x < log 1 3 3 - x ?
A. 1
B. 2
C. 3
D. 4
Chọn B.
Xét bất phương trình 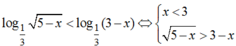
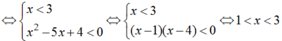
Mặt khác x + 1/3 là số nguyên ![]() là số nguyên khi 3x + 1 chia hết cho 3.
là số nguyên khi 3x + 1 chia hết cho 3.
Ta có ![]()

Vậy có tất cả 2 giá trị của x thỏa mãn yêu cầu bài toán.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của x thỏa mãn: |6 - 2(x + 2)| = 2 - 2x.
A. x = 1
B. x < 1
C. x ≤ 1
D. x > 1
có bao nhiêu x thảo mãn (x+2).(2x-4)<0
\(\left(x+2\right)\left(2x-4\right)< 0\)
\(\Leftrightarrow2\left(x+2\right)\left(x-2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2>0\\x-2< 0\end{matrix}\right.\\\left\{{}\begin{matrix}x+2< 0\\x-2>0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}-2< x< 2\left(tm\right)\\2< x< -2\left(VLý\right)\end{matrix}\right.\)
Vì \(x\in N\)
\(\Rightarrow x\in\left\{0;1\right\}\)
Đúng 2
Bình luận (2)
Cho hàm số \(y=-2x^3+(2m-1)x^2-(m^2-1)x+2\). Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho có hai điểm cực trị?
\(y'=-6x^2+2\left(2m-1\right)x-\left(m^2-1\right)\)
Hàm có 2 cực trị khi:
\(\Delta'=\left(2m-1\right)^2-6\left(m^2-1\right)>0\)
\(\Rightarrow-2m^2-4m+7>0\)
\(\Rightarrow-\dfrac{2+3\sqrt{2}}{2}< m< \dfrac{-2+3\sqrt{2}}{2}\)
\(\Rightarrow m=\left\{-3;-2;-1;0;1\right\}\)
Đúng 2
Bình luận (0)