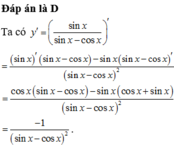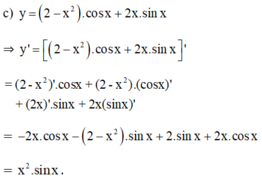Câu 1 : tính đạo hàng của hàm số sau : a, y = 1/| cosx |
HH
Những câu hỏi liên quan
Tính đạo hàm của hàm số sau
y
sin
x
sin
x
-
cos
x
A.
y
-
1
sin
x
+
cos
x
2...
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
A. y ' = - 1 sin x + cos x 2
B. y ' = 1 sin x - cos x 2
C. y ' = 1 sin x + cos x 2
D. y ' = - 1 sin x - cos x 2
Tính đạo hàm của hàm số sau
y
sin
x
sin
x
−
cos
x
A.
y
−
1
sin
x
−
cos
x...
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x sin x − cos x
A. y ' = − 1 sin x − cos x 2
B. y ' = 1 sin x − cos x 2
C. y ' = − 1 sin x + cos x 2
D. y ' = 1 sin x + cos x 2
Đáp án A
Ta có y ' = cos x sin x − cos x − cos x + sin x sin x sin x − cos x 2 = − cos 2 x − sin 2 x sin x − cos x 2 = − 1 sin x − cos x 2
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau
y
sin
x
+
cos
x
sin
x
−
cos
x
A.
−
2
sin
x
(
sin
x...
Đọc tiếp
Tính đạo hàm của hàm số sau y = sin x + cos x sin x − cos x
A. − 2 sin x ( sin x − cos x ) 2
B. 2 c osx ( sin x − cos x ) 2
C. − 2 ( sin x − cos x ) 2
D. − 2 s inx + c osx ( sin x − cos x ) 2
y ' = sin x + cos x sin x − cos x ' = ( sin x + cos x ) ' . ( sin x − cos x ) − ( sin x − cos x ) ' . ( sin x + cos x ) ( sin x − cos x ) 2 = ( cos x − sin x ) ( sin x − cos x ) − ( cos x + sin x ) ( sin x + cos x ) ( sin x − cos x ) 2 = − ( cos x − sin x ) ( − sin x + cos x ) − ( sin x + cos x ) ( sin x + cos x ) ( sin x − cos x ) 2
= − ( cos x − sin x ) 2 − ( sin x + cos x ) 2 ( sin x − cos x ) 2 = − ( cos 2 x − 2 cos x sin x + sin 2 x ) − ( sin 2 x + 2 sin x cos x + cos 2 x ) ( sin x − cos x ) 2 = − ( 1 − 2 cos x sin x ) − ( 1 + 2 sin x cos x ) ( sin x − cos x ) 2
= − 2 ( sin x − cos x ) 2
Chọn đáp án C
Đúng 0
Bình luận (0)
Câu 1: Tính giới hạn: lim (xrightarrow-1)dfrac{2x^2-x-3}{x^2-1}Câu 2: Tính đạo hàm của hàm số sau:a. y2x3-cosx-sqrt{x}+2020 b. y(x2-5)10Câu 3:Viết phương trình tiếp tuyến của đồ thị (C): y-x2-20, biết tiếp tuyến có hệ số góc k4.Câu 4 Cho hàm số:yx.sinx. Chứng minh: y+yn-x.(cosx-sinx)sinx+2cos
Đọc tiếp
Câu 1: Tính giới hạn: lim (x\(\rightarrow\)-1)\(\dfrac{2x^2-x-3}{x^2-1}\)
Câu 2: Tính đạo hàm của hàm số sau:
a. y=2x3-cosx-\(\sqrt{x}\)+2020 b. y=(x2-5)10
Câu 3:Viết phương trình tiếp tuyến của đồ thị (C): y=-x2-20, biết tiếp tuyến có hệ số góc k=4.
Câu 4 Cho hàm số:y=x.sinx. Chứng minh: y'+yn-x.(cosx-sinx)=sinx+2cos
1.
\(\lim\limits_{x\rightarrow-1}\dfrac{2x^2-x-3}{x^2-1}=\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(2x-3\right)}{\left(x+1\right)\left(x-1\right)}=\lim\limits_{x\rightarrow-1}\dfrac{2x-3}{x-1}=\dfrac{5}{2}\)
2.
a. \(y'=6x^2-sinx-\dfrac{1}{2\sqrt{x}}\)
b. \(y'=10\left(x^2-5\right)^9.\left(x^2-5\right)'=20x\left(x^2-5\right)^9\)
3.
\(y'=-2x\)
\(k=4\Rightarrow-2x=4\Rightarrow x=-2\Rightarrow y\left(-2\right)=-24\)
Phương trình tiếp tuyến:
\(y=4\left(x+2\right)-24\Leftrightarrow y=4x-16\)
Đúng 0
Bình luận (0)
Tìm đạo hàm cấp hai của hàm số sau: y = ( 1 - x 2 ) cos x
y ′ ′ = ( x 2 − 3 ) cos x + 4 x sin x .
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau: y = 2 - x 2 . cos x + 2 x . sin x
cíuuuuuuu em với phần đạo hàm cấp n của các hàm số sau:
1.\(y=sinax\) 2.\(y=cosax\)
\(3.y=sin3x\cdot cosx\) \(4.y=cos5x\cdot cosx\)
a) Tính đạo hàm của hàm số \(y=\sqrt{sinx+cosx}\)
b) Hãy viết phương trình tiếp tuyến với đồ thị (C) của hàm số \(y=\dfrac{x+3}{x-1}\) biết tiếp tuyến vuông góc với đường thẳng \(y=\dfrac{1}{4}x+5\)
a.
\(y'=\dfrac{\left(sinx+cosx\right)'}{2\sqrt{sinx+cosx}}=\dfrac{cosx-sinx}{2\sqrt{sinx+cosx}}\)
b.
\(y'=\dfrac{-4}{\left(x-1\right)^2}\)
Tiếp tuyến vuông góc với \(y=\dfrac{1}{4}x+5\) nên có hệ số góc thỏa mãn \(k.\left(\dfrac{1}{4}\right)=-1\Rightarrow k=-4\)
\(\Rightarrow\dfrac{-4}{\left(x-1\right)^2}=-4\Rightarrow\left(x-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-3\\x=2\Rightarrow y=5\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn: \(\left[{}\begin{matrix}y=-4x-3\\y=-4\left(x-2\right)+5\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tính đạo hàm của hàm số
y
sin
x
sin
x
-
cos
x
A.
y
-
1
sin
x
-
cos
x
2...
Đọc tiếp
Tính đạo hàm của hàm số y = sin x sin x - cos x
A. y ' = - 1 sin x - cos x 2
B. y ' = 1 sin x - cos x 2
C. y ' = - 1 sin x + cos x 2
D. y ' = 1 sin x + cos x 2