Giải giúp mình với. Cảm ơn nhiều!
TT
Những câu hỏi liên quan
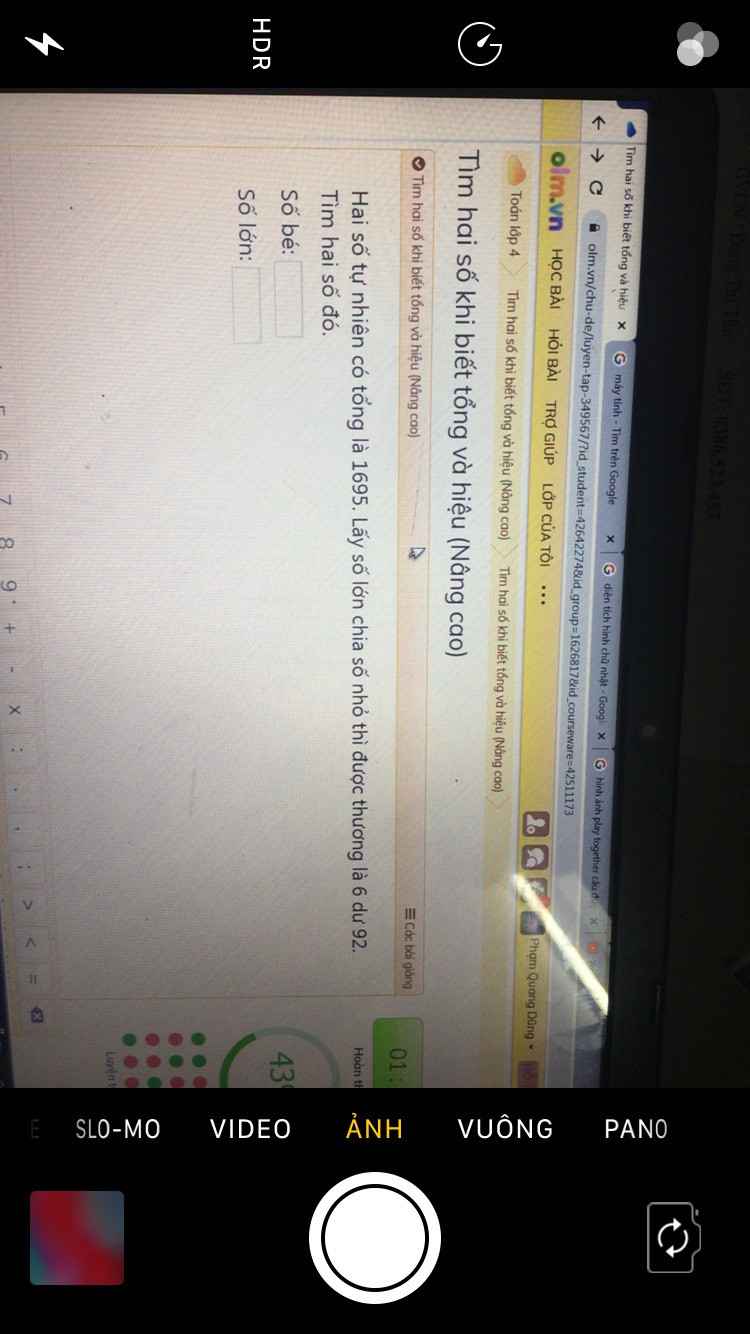 giải giúp mình với mình cảm ơn nhiều
giải giúp mình với mình cảm ơn nhiều
giải giúp mình với ạ, mình cảm ơn nhiều 
a: HB=4,5(cm)
BC=12,5(cm)
b: \(\widehat{B}=37^0\)
Đúng 0
Bình luận (0)
Giúp mình với ạ, giải chi tiết giúp mình nha mình cảm ơn nhiều!!
 giải giúp mình với, cảm ơn nhiều
giải giúp mình với, cảm ơn nhiều
a) Xét tứ giác ADHE có
\(\widehat{ADH}\) và \(\widehat{AEH}\) là hai góc đối
\(\widehat{ADH}+\widehat{AEH}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADHE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 1
Bình luận (0)
a) Xét tứ giác BDEC có
\(\widehat{BDC}=\widehat{BEC}\left(=90^0\right)\)
\(\widehat{BDC}\) và \(\widehat{BEC}\) là hai góc cùng nhìn cạnh BC
Do đó: BDEC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
b) Ta có: BDEC là tứ giác nội tiếp(cmt)
nên \(\widehat{DEB}=\widehat{DCB}\)(hai góc nội tiếp cùng chắn cung BD)
hay \(\widehat{KEB}=\widehat{KCD}\)
Xét ΔKEB và ΔKCD có
\(\widehat{KEB}=\widehat{KCD}\)(cmt)
\(\widehat{DKB}\) chung
Do đó: ΔKEB\(\sim\)ΔKCD(g-g)
Suy ra: \(\dfrac{KE}{KC}=\dfrac{KB}{KD}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(KD\cdot KE=KB\cdot KC\)(đpcm)
Đúng 0
Bình luận (0)
Giải giúp mình nó với ạ. Mình cảm ơn nhiều
Đọc tiếp
Giải giúp mình nó với ạ. Mình cảm ơn nhiều







Giúp mình với ạ, giải thích chi tiết giúp mình nha, mình cảm ơn nhiều!!
Giải giúp mình với ạ, mình cần gấp, cảm ơn nhiều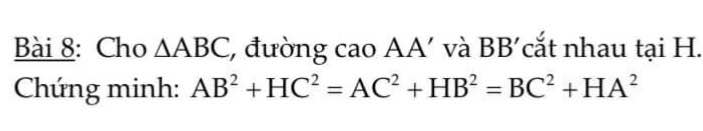
Ta có: \(AB^2+HC^2=\left(AA'^2+A'B^2\right)+\left(A'H^2+A'C^2\right)\)
\(=\left(AA'^2+A'C^2\right)+\left(A'B^2+A'H^2\right)=AC^2+HB^2\)
Lại có: \(BC^2+HA^2=\left(BB'^2+B'C^2\right)+\left(B'H^2+B'A^2\right)\)
\(=\left(BB'^2+B'A^2\right)+\left(B'C^2+B'H^2\right)=AB^2+HC^2\)
\(\Rightarrow AB^2+HC^2=AC^2+HB^2=BC^2+HA^2\)
Đúng 2
Bình luận (0)
Giải giúp mình với ạ, cảm ơn nhiều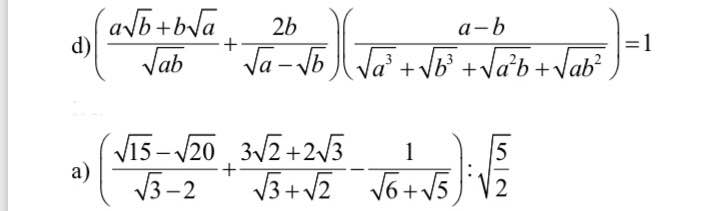
d) Ta có: \(\left(\dfrac{a\sqrt{b}+b\sqrt{a}}{\sqrt{ab}}+\dfrac{2b}{\sqrt{a}-\sqrt{b}}\right)\left(\dfrac{a-b}{\sqrt{a^3}+\sqrt{b^3}+\sqrt{a^2b}+\sqrt{ab^2}}\right)\)
\(=\left(\sqrt{a}+\sqrt{b}+\dfrac{2b}{\sqrt{a}-\sqrt{b}}\right)\cdot\left(\dfrac{a-b}{a\sqrt{a}+b\sqrt{b}+a\sqrt{b}+b\sqrt{a}}\right)\)
\(=\dfrac{a-b+2b}{\sqrt{a}-\sqrt{b}}\cdot\dfrac{a-b}{\left(\sqrt{a}+\sqrt{b}\right)\left(a+b\right)}\)
\(=\dfrac{\left(a+b\right)\cdot\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\left(a+b\right)\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}\)
=1
Đúng 0
Bình luận (1)
Giải giúp mình câu 6 với. Mình cần gấp. Cảm ơn nhiều.
\(\Leftrightarrow16x^4-4x^2-4xy+y^2+1=0\)
\(\Leftrightarrow\left(16x^4-8x^2+1\right)+\left(4x^2-4xy+y^2\right)=0\)
\(\Leftrightarrow\left(4x^2-1\right)^2+\left(2x-y\right)^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x^2-1=0\\2x-y=0\end{matrix}\right.\)
\(\Leftrightarrow\left(x;y\right)=\left(-\dfrac{1}{2};-1\right);\left(\dfrac{1}{2};1\right)\)
Đúng 3
Bình luận (0)


