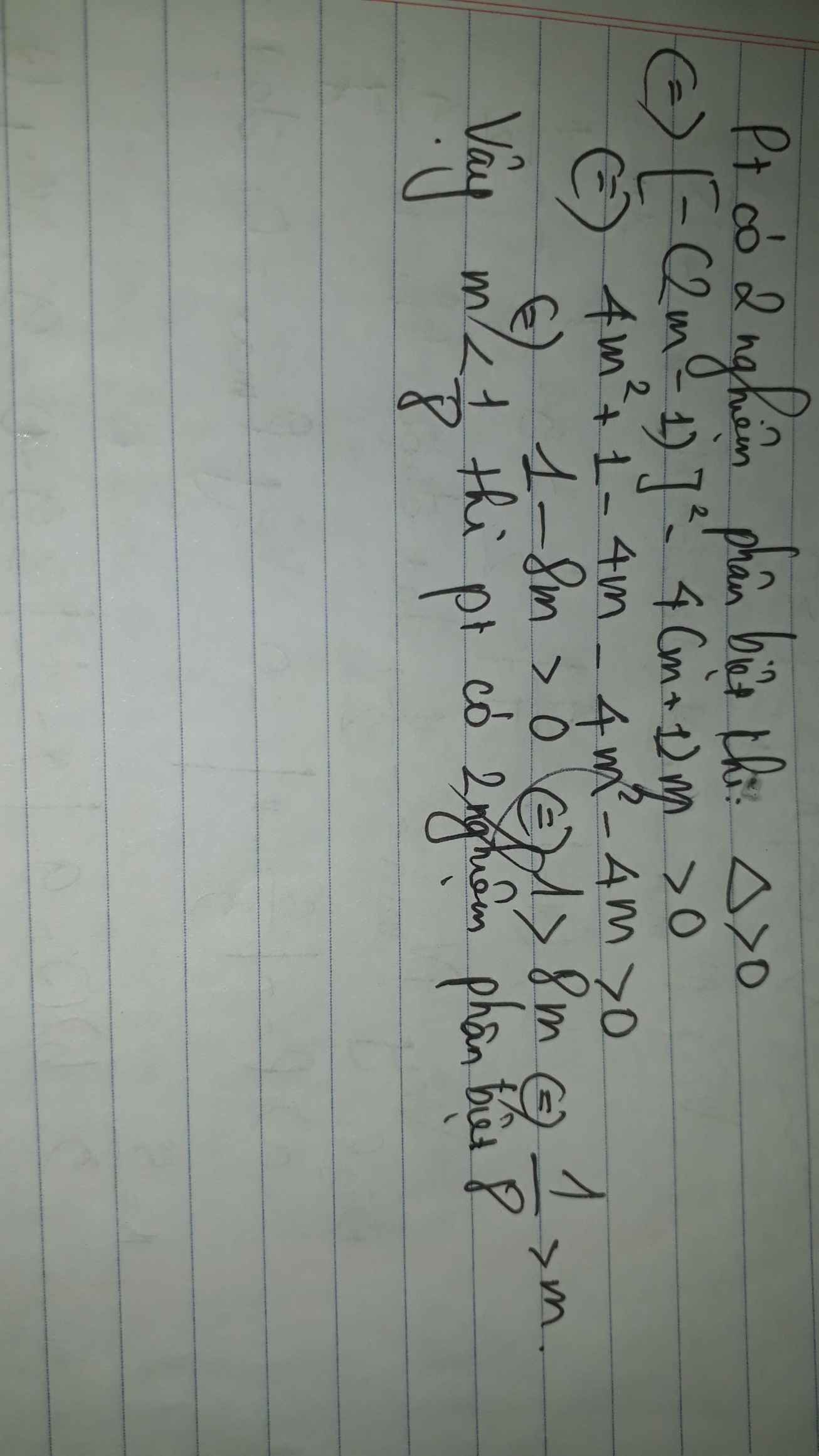Đáp án A: \(x + y > 3\) là bất phương trình bậc nhất hai ẩn x và y có a=1, b=1, c=3

Đáp án B: \({x^2} + {y^2} \le 4\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)

Đáp án C: \(\left( {x - y} \right)\left( {3x + y} \right) \ge 1 \Leftrightarrow 3{x^2} - 2xy - {y^2} \ge 1\) không là bất phương trình bậc nhất hai ẩn vì có \({x^2},{y^2}\)

Đáp án D: \({y^3} - 2 \le 0\) không là bất phương trình bậc nhất hai ẩn vì có \({y^3}\).

Chọn A

A

A

A

a. Với \(m=-5\) pt trở thành:

\(x^2+8x-9=0\)

\(a+b+c=1+8-9=0\) nên pt có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=1\\x_2=-9\end{matrix}\right.\)

b. Ta có:

\(\Delta'=\left(m+1\right)^2-\left(m-4\right)=m^2+m+5=\left(m+\dfrac{1}{2}\right)^2+\dfrac{19}{4}>0;\forall m\)

\(\Rightarrow\) Pt đã cho luôn có 2 nghiệm pb với mọi m

Ta có: \(\text{Δ}=\left(1-4m\right)^2-4\left(3-2m\right)\left(1-2m\right)\)

\(=16m^2-8m+4-4\left(2m-3\right)\left(2m-1\right)\)

\(=16m^2-8m+4-4\left(4m^2-2m-6m+3\right)\)

\(=16m^2-8m+4-4\left(4m^2-8m+3\right)\)

\(=16m^2-8m+4-16m^2+32m-12\)

\(=24m-8\)

Để phương trình có hai nghiệm phân biệt thì

\(\left\{{}\begin{matrix}3-2m\ne0\\24m-8>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2m\ne3\\24m>8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{3}{2}\\m>\dfrac{1}{3}\end{matrix}\right.\)

minh moi hok lop 6

\(\Delta=\left(2m-1\right)^2-4\cdot\left(m+1\right)\cdot m\)

\(=4m^2-4m+4-4m^2-4m\)

\(=-8m+4\)

Để phương trình có hai nghiệm phân biệt thì 

\(\left\{{}\begin{matrix}m+1\ne0\\-8m+4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\-8m>-4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m< \dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m< \dfrac{1}{2}\)

Để phương trình có 2 nghiệm x₁,x₂

\(\Leftrightarrow\Delta=\left(m-2\right)^2-4\cdot\left(-2m\right)\ge0\)

\(\Leftrightarrow m^2-4m+4+8m\ge0\)

\(\Leftrightarrow\left(m+2\right)^2\ge0\) (luôn đúng)

Theo định lí Vi-ét:

\(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=-2m\end{matrix}\right.\)

Kết hợp định lí Vi-ét và đề bài ta có điều kiện:

\(\left\{{}\begin{matrix}x_1+x_2=m-2\\2x_1+3x_2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1=m-2-x_2\\2\left(m-2-x_2\right)+3x_2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_1=m-2-x_2\\2m-4-2x_2+3x_2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=3m-6\\x_2=4-2m\end{matrix}\right.\)

Cũng theo Vi-ét:

\(x_1x_2=-2m\) \(\Rightarrow\left(3m-6\right)\left(4-2m\right)=-2m\)

\(\Rightarrow-6m^2+26m-24=0\)

\(\Rightarrow\left[{}\begin{matrix}m=3\\m=\dfrac{4}{3}\end{matrix}\right.\)

Vậy \(m\in\left\{3;\dfrac{4}{3}\right\}\) thỏa mãn đề

Tick nha 😘

\(\Delta=\left(m-2\right)^2+8m=\left(m+2\right)^2\ge0;\forall m\Rightarrow\) phương trình đã cho luôn có nghiệm

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=-2m\end{matrix}\right.\)

Kết hợp hệ thức Viet và điều kiện đề bài ta được:

\(\left\{{}\begin{matrix}x_1+x_2=m-2\\2x_1+3x_2=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=2m-4\\2x_1+3x_2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_1=3m-6\\x_2=-2m+4\end{matrix}\right.\)

Thế vào \(x_1x_2=-2m\)

\(\Rightarrow\left(3m-6\right)\left(-2m+4\right)=-2m\)

\(\Leftrightarrow-6m^2+26m-24=0\Rightarrow\left[{}\begin{matrix}m=3\\m=\dfrac{4}{3}\end{matrix}\right.\)

\(a,PT\Leftrightarrow\left(1-2m\right)x=m+4\)

Bậc nhất \(\Leftrightarrow1-2m\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)

\(b,x=2\Leftrightarrow2-4m-m-4=0\Leftrightarrow m=-\dfrac{2}{5}\\ c,m=5\Leftrightarrow-9x-9=0\Leftrightarrow x=-1\)

cứu mik với

 a, \(x^2-\left(2m+1\right)x+m^2+5m=0\)

Với m=2 

\(x^2-\left[2.\left(-2\right)+1\right]x+\left(-2\right)^2+5.\left(-2\right)=0\)

\(x^2+3x-6=0\)

\(\Delta=3^2-4.1.\left(-6\right)\)

     \(=9+24\)

\(=33>0\Rightarrow\sqrt{\Delta}=\sqrt{33}\)

\(\Rightarrow\)Phương trình có 2 nghiệm phân biệt:

\(x_1=\dfrac{-3+\sqrt{33}}{2}\)

\(x_2=\dfrac{-3-\sqrt{33}}{2}\)

Vậy khi m=-2 thì phương trình có nghiệm là \(x_1=\dfrac{-3+\sqrt{33}}{2};x_2=\dfrac{-3-\sqrt{33}}{2}\)

b,Ta có \(\Delta=\left[-\left(2m+1\right)\right]^2-4\left(m^2+5m\right)\)

                 \(=4m^2+4m+1-4m^2-20m\)

                 \(=1-16m\)

Phương trình có 2 nghiệm\(\Leftrightarrow\Delta\ge0\)

                                          \(\Leftrightarrow1-16m\ge0\)

                                          \(\Leftrightarrow m\le\dfrac{1}{16}\)

Khi đó hệ thức viet ta có tích các nghiệm là\(m^2+5m\)

Mà tích các nghiệm bằng 6, do đó \(m^2+5m=6\)

                                                   \(\Leftrightarrow m^2+5m-6=0\)

Ta thấy \(a+b+c=1+5+\left(-6\right)=0\) nên \(m_1=1;m_2=-6\)

Đối chiếu với điều kiện \(m\le\dfrac{1}{16}\) thì \(m=-6\) là giá trị cần tìm

-Chúc bạn học tốt-