gọi x là vận tốc khi xuôi dòng( x>0) (km/h)
gọi y là vận tốc ngược dòng(y>0) (km/h)
*, ca nô chạy trên sông trong 8 giờ:
xuôi dòng 81km:81/x và ngược dòng 105km: 105/y
=> phương trinh: 81/x + 105/y=8    (1)
*,ca nô chạy trong 4 giờ:
xuôi dòng 54km: 54/x và ngược dòng 42km: 42/y
=> ph trình: 54/x + 42/y = 4    (2)
từ (1) và (2) ta có hệ pt:
....
....
..... => x=27km/h
y=21km/h

V xuôi : 27km/h

V ngược : 21km/h

Trả lời : 

V xuôi : 27 km/giờ

V ngược 21 km/giờ

Hok tốt!

Gọi vận tốc cano là x (km/h,x>0) và vận tốc dòng nước là y(km/h,y>0)

Vận tốc cano xuôi dòng là x+y(km/h)

Vận tốc cano ngược dòng là x-y(km/h)

thời gian cano xuôi dòng khúc sông 60km là \(\frac{60}{x+y}\)

       Thời gian cano ngược dòng 48km là \(\frac{48}{x-y}\)

tổng thời gian là 6h nên ta có pt: \(\frac{60}{x+y}\)+\(\frac{48}{x-y}\)=6

Tưiong tự ta có pt \(\frac{40}{x+y}\)+\(\frac{80}{x-y}\)=7

Ta có hpt \(\hept{\begin{cases}\frac{60}{x+y}+\frac{48}{x-y}=6\\\frac{40}{x+y}+\frac{80}{x-y}=7\end{cases}}\)

Đặt ẩn phụ giải ra ta đc \(\hept{\begin{cases}x+y=20\\x-y=16\end{cases}}\)

nên x=18,y=2

kl

Gọi vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là x, y (km/h; x > y > 0)

Suy ra vận tốc xuôi dòng của ca nô là x + y(km/h); vận tốc ngược dòng là x – y (km/h)

Ca nô chạy trên sông trong 8h xuôi dòng được 81 km và ngược dòng 105 km nên ta có phương trình: 81 x + y + 105 x - y = 8  (1)

Ca nô chạy trên sông trong 4h xuôi dòng được 54km và ngược dòng 42km nên ta có phương trình: 54 x + y + 42 x - y = 4  (2)

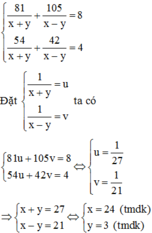
Vậy vận tốc riêng của ca nô và vận tốc dòng nước lần lượt là 24 km/h và 3 km/h

Đáp án: D

Gọi \(a,b\) lần lượt là vận tốc riêng của ca nô và vận tốc dòng nước \(\left(a>b>0\right)\).

Thời gian ca nô đi xuôi dòng khúc sông \(60km\) là : \(\dfrac{60}{a+b}\left(h\right)\).

Thời gian ca nô đi ngược dòng \(48km\) là : \(\dfrac{48}{a-b}\left(h\right)\).

Theo đề bài thì \(\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\left(1\right)\).

Thời gian ca nô đi xuôi dòng \(40km\) là : \(\dfrac{40}{a+b}\left(h\right)\).

Thời gian ca nô đi ngược dòng \(80km\) là : \(\dfrac{80}{a-b}\left(h\right)\)

Cũng theo đề bài, ta có : \(\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\left(2\right)\).

Từ \((1)\) và \((2)\), ta có hệ phương trình : 

\(\left\{{}\begin{matrix}\dfrac{60}{a+b}+\dfrac{48}{a-b}=6\\\dfrac{40}{a+b}+\dfrac{80}{a-b}=7\end{matrix}\right.\left(I\right)\)

Đặt : \(x=\dfrac{20}{a+b}\) và \(y=\dfrac{16}{a-b}\). Hệ \((I)\) được viết lại thành : 

\(\left\{{}\begin{matrix}3x+3y=6\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=2\\2x+5y=7\end{matrix}\right.\)

Hay : \(\left\{{}\begin{matrix}5x+5y=10\\2x+5y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=3\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{20}{a+b}=1\\\dfrac{16}{a-b}=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a+b=20\\a-b=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=36\\a+b=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=18\\b=2\end{matrix}\right.\) (thỏa mãn).

Vậy : Vận tốc riêng của ca nô là \(18(km/h)\) và vận tốc dòng nước là \(2(km/h).\)

Gọi vận tốc riêng của cano là x (km/h) với x>0

Gọi vận tốc của dòng nước là y (km/h) với y>0 và y<x

Vận tốc cano khi xuôi dòng: \(x+y\) (km/h)

Vận tốc cano khi ngược dòng: \(x-y\) (km/h)

Do cano xuôi dòng 60km và ngược dòng 48km hết 6h nên ta có:

\(\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\)

Do cano xuôi dòng 40km và ngược dòng 80km thì hết 7h nên ta có:

\(\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\)

Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{120}{x+y}+\dfrac{240}{x-y}=21\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{120}{x+y}+\dfrac{96}{x-y}=12\\\dfrac{144}{x-y}=9\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x-y=16\\\dfrac{120}{x+y}+\dfrac{96}{16}=12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x-y=16\\x+y=20\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=18\\y=2\end{matrix}\right.\)

Gọi x (km/h) là vận tốc riêng của cano.(x>0)

Gọi y (km/h) là vận tốc dòng nước.(y>0)

Theo đề bài ta có hệ phương trình:

\(\hept{\begin{cases}\frac{81}{x+y}+\frac{105}{x-y}=8\\\frac{54}{x+y}+\frac{42}{x-y}=4\end{cases}}\)

Giải ra ta được:

\(\hept{\begin{cases}x+y=27\\x-y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=24\\y=3\end{cases}}}\)

Vậy vận tốc riêng của cano là 24km/h.

Vận tốc dòng nước là 3km/h

Gọi vận tốc riêng của cano là \(x\left(km/h\right),x>4\).

Vận tốc khi cano đi xuôi dòng là: \(x+4\left(km/h\right)\).

Thời gian cano đi xuôi dòng là: \(\frac{120}{x+4}\left(h\right)\).

Vận tốc khi cano đi ngược dòng là: \(x-4\left(km/h\right)\).

Thời gian cano đi ngược dòng là: \(\frac{96}{x-4}\left(h\right)\).

Ta có phương trình:

\(\frac{96}{x-4}-\frac{120}{x+4}=1\)

\(\Rightarrow96\left(x+4\right)-120\left(x-4\right)=\left(x-4\right)\left(x+4\right)\)

\(\Leftrightarrow x^2+24x-880=0\)

\(\Leftrightarrow x=20\)(vì \(x>4\)) 

.

gọi vận tốc ca nô xuôi dòng là x+y(km/h)(x>0)

vận tốc ca nô ngược dòng là :x-y(km/h)(y>0)(x>y)

ta có hệ pt: \(\left\{{}\begin{matrix}\dfrac{60}{x+y}+\dfrac{48}{x-y}=6\\\dfrac{40}{x+y}+\dfrac{80}{x-y}=7\end{matrix}\right.\)

giải hệ pt trên bằng cách đặt\(\dfrac{1}{x+y}=a\) và \(\dfrac{1}{x-y}=b\)

=>\(\left\{{}\begin{matrix}60a+48b=6\\40a+80b=7\end{matrix}\right.\) giải hệ pt này =>\(\left\{{}\begin{matrix}a=\dfrac{1}{20}\\b=\dfrac{1}{16}\end{matrix}\right.\)=>\(\left\{{}\begin{matrix}\dfrac{1}{x+y}=\dfrac{1}{20}\\\dfrac{1}{x-y}=\dfrac{1}{16}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+y=20\\x-y=16\end{matrix}\right.< =>\left\{{}\begin{matrix}x=18\left(TM\right)\\y=2\left(TM\right)\end{matrix}\right.\)

vậy vận tốc riêng ca nô là 18km/h , vận tốc dòng nước là 2km/h

Gọi quãng AB là : x 

Vận tốc lúc xuôi dòng là : \(\frac{x}{5}\) km/h 

Vận tốc lúc ngược là : \(\frac{x}{6}\)km/h 

Theo bài ra ta có : \(\frac{x}{5}-\frac{x}{6}=6\)

\(\Leftrightarrow6x-5x=180\)

x = 180 

Vậy AB dài 180 km