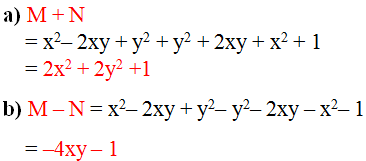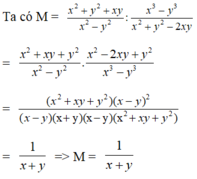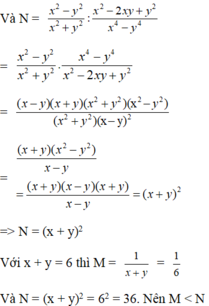M=x²-2xy+y² N=y²+2xy+x²+1 Tính M+N và M-N
H24
Những câu hỏi liên quan
Cho hai đa thức M = x2 y - 2xy + 6 - xy và N = -2x2 y + 2xy +x2 y - 3
a) Thu gọn M và N.
b) Tính M khi x=1 và y=2
c) Tính M+N
a) \(\left\{{}\begin{matrix}M=x^2y-2xy+6-xy=x^2y-3xy+6\\N=-2x^2y+2xy+x^2y-3=-x^2y+2xy-3\end{matrix}\right.\)
b) \(x=1;y=2\Rightarrow M=1^2.2-2.1.2+6-1.2=2\)
c) \(M+N\Rightarrow x^2y-3xy+6+\left(-x^2y\right)+2xy-3=-xy+3\)
Đúng 2
Bình luận (0)
Tính tổng và hiệu của 2 đa thức M và N
a)M= x^2 + y^2 + 2xy và N= x^2 + y^2 - 2xy
b)M = 2,3x + 3,2y - 10 và N= -0,3x + 2,2y - 5
1. phân tích đa thức thành nhân tử:
e, x(y-x)^2 -x^2+2xy-y^2
2. tính gt biểu thức
a, M= m^2(m+n)-n^2m-n^3 tại m= -2017 và n=2017
Bài 1:
e: Ta có: \(x\left(y-x\right)^2-x^2+2xy-y^2\)
\(=x\left(x-y\right)^2-\left(x-y\right)^2\)
\(=\left(x-y\right)^2\cdot\left(x-1\right)\)
Đúng 1
Bình luận (0)
Bài 2:
a: Ta có: \(M=m^2\left(m+n\right)-n^2m-n^3\)
\(=m^2\left(m+n\right)-n^2\left(m+n\right)\)
\(=\left(m+n\right)^2\cdot\left(m-n\right)\)
\(=\left(-2017+2017\right)^2\cdot\left(-2017-2017\right)\)
=0
Đúng 1
Bình luận (1)
Cho hai đa thức :
\(M=x^2-2xy+y^2\)
\(N=y^2+2xy+x^2+1\)
a) Tính M + N
b) Tính M - N
M + N = \(x^2-2xy+y^2\)+\(y^2+2xy+x^2+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
= \(2x^2+2y^2+1\)
M - N = \(x^2-2xy+y^2-y^2+2xy+1\)
= \(\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2-y^2\right)+1\)
= \(2x^2+1\)
Đúng 0
Bình luận (0)
Cho hai đa thức:
M = x2 – 2xy + y2;
N = y2 + 2xy + x2 + 1.
a) Tính M + N;
b) Tính M - N.
a) M + N = x2 – 2xy + y2+ y2 + 2xy + x2 + 1 = 2x2 + 2y2+ 1
b) M - N = x2 – 2xy + y2 - y2 - 2xy - x2 - 1 = -4xy - 1.
Học tốt
Đúng 0
Bình luận (0)
Cho hai đa thức:
M = x2 – 2xy + y2;
N = y2 + 2xy + x2 + 1.
a) Tính M + N;
b) Tính M - N.
a/ M + N = x\(^2\)- 2xy + y\(^2\)+ y\(^2\)+ 2xy + x\(^2\)+ 1
= 2x\(^2\)+ 2y\(^2\)+ 1
= 2( x\(^2\)+ y\(^2\)) + 1
b/ M - N = x\(^2\)- 2xy + y\(^2\)- ( y\(^2\)+ 2xy + x\(^2\)+ 1 )
= x\(^2\)- 2xy + y\(^2\)- y\(^2\)- 2xy - x\(^2\)- 1
= -4xy - 1
Đúng 0
Bình luận (0)
cho 2 đa thức
M=x2-2xy+y2
N=Y2+2xy+x2+1
a. tính M+N
b. tính M-N
GIÚP MIK NHA AI NHANH MIK TÍCH
\(M=x^2-2xy+y^2\)
\(N=y^2+2xy+x^2+1\)
\(a,M+N=\left(x^2-2xy+y^2\right)+\left(y^2+2xy+x^2+1\right)\)
\(=x^2-2xy+y^2+y^2+2xy+x^2+1\)
\(=\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
\(=2x^2+2y^2+1\)
\(b,M-N=\left(x^2-2xy+y^2\right)-\left(y^2+2xy+x^2+1\right)\)
\(=x^2-2xy+y^2-y^2-2xy-x^2-1\)
\(=\left(x^2-x^2\right)+\left(-2xy-2xy\right)+\left(y^2-y^2\right)-1\)
\(=-4xy-1\)
Đúng 0
Bình luận (0)
cho hai đa thức :
M = \(x^2-2xy+y^2\)
N = \(y^2+2xy+x^2+1\)
a, Tính M + N
b, tính M - N
a, M + N = \(\left(x^2-2xy+y^2\right)+\left(y^2+2xy+x^2+1\right)\)
=\(2x^2+2y^2+1\)
b,M - N =\(\left(x^2-2xy+y^2\right)-\left(y^2+2xy+x^2+1\right)\)
=\(-4xy-1\)
Đúng 0
Bình luận (0)
\(M+N=\left(x^2-2xy+y^2\right)+\left(y^2+2xy+x^2+1\right)\)
\(\Rightarrow M+N=2x^2+2y^2+1\)
\(M-N=\left(x^2-2xy+y^2\right)-\left(y^2+2xy+x^2+1\right)\)
\(\Rightarrow M-N=-4xy-1\)
tíc mình nha
Đúng 0
Bình luận (0)
\(a.M+N=\left(x^2-2xy+y^2\right)+\left(y^2+2xy+x^2+1\right)\)
\(=x^2-2xy+y^2+y^2+2xy+x^2+1\)
\(=\left(x^2+x^2\right)+\left(-2xy+2xy\right)+\left(y^2+y^2\right)+1\)
\(=2x^2+2y^2+1\)
\(b.M-N=\left(x^2-2xy+y^2\right)-\left(y^2+2xy+x^2+1\right)\)
\(=x^2-2xy+y^2-y^2-2xy-x^2-1\)
\(=\left(x^2-x^2\right)+\left(-2xy-2xy\right)+\left(y^2-y^2\right)-1\)
\(=-4xy-1\)
T mk nhé bn ^...^ ^_^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho M
x
2
+
y
2
+
x
y
x
2
−
y
2
:
x
3
−
y...
Đọc tiếp
Cho M = x 2 + y 2 + x y x 2 − y 2 : x 3 − y 3 x 2 + y 2 − 2 x y và N = x 2 − y 2 x 2 + y 2 : x 2 − 2 x y + y 2 x 4 − y 4 . Khi x + y = 6, hãy so sánh M và N
A. M < N
B. M > N
C. M ≥ N
D. M = N