Câu 1 và 2 ở phần 2 nhé mn 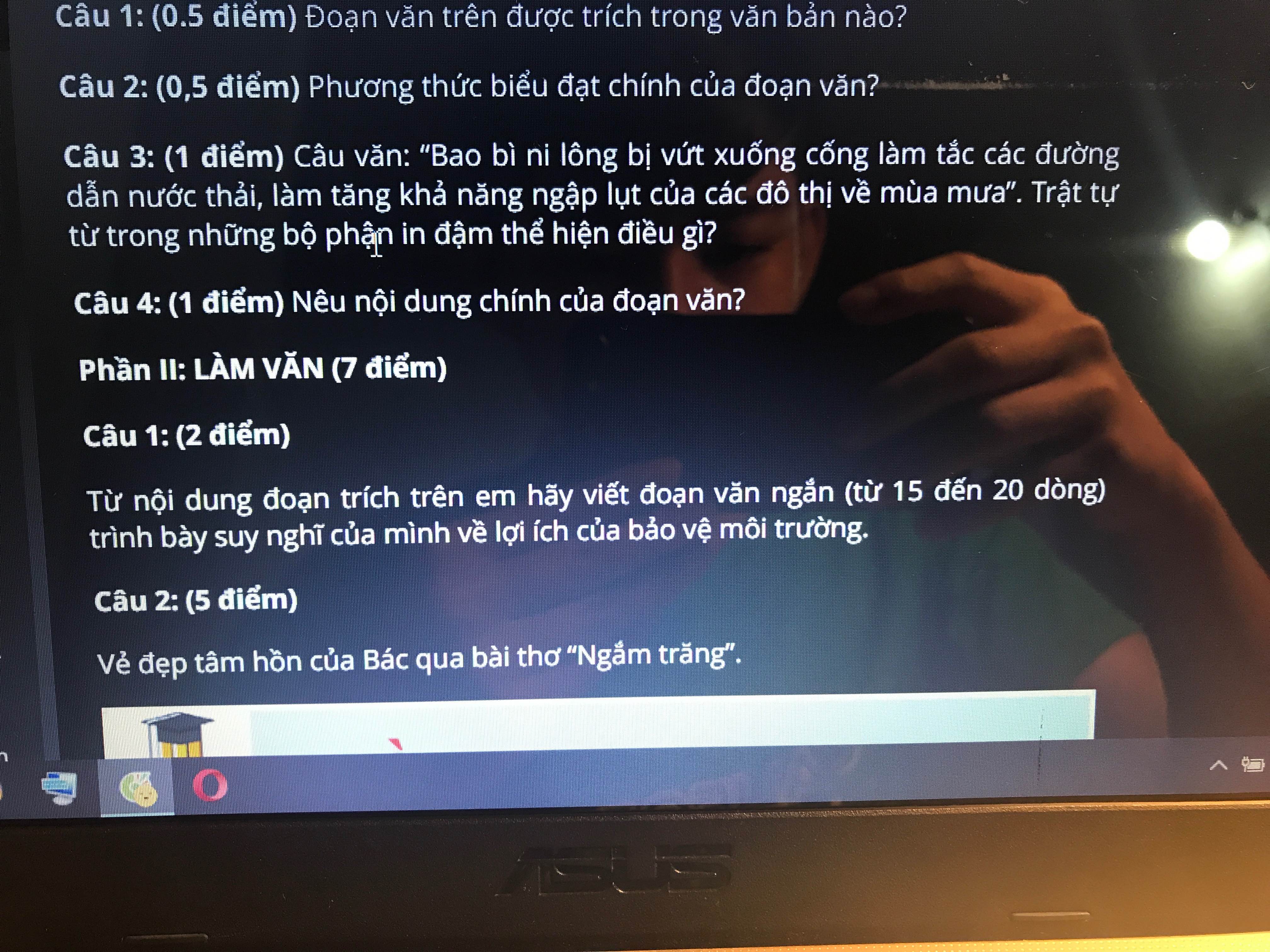
MP
Những câu hỏi liên quan
Giúp Mik câu không ở phần vận dụng đâu nhé , Câu 2 đầu tiên nha
Câu 1 với câu 3 phần 1 mình giải đc rồi nhưng còn câu còn lại và câu 3 phần 2 chưa giải được mong các bạn, anh chị giúp mình nhé

Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
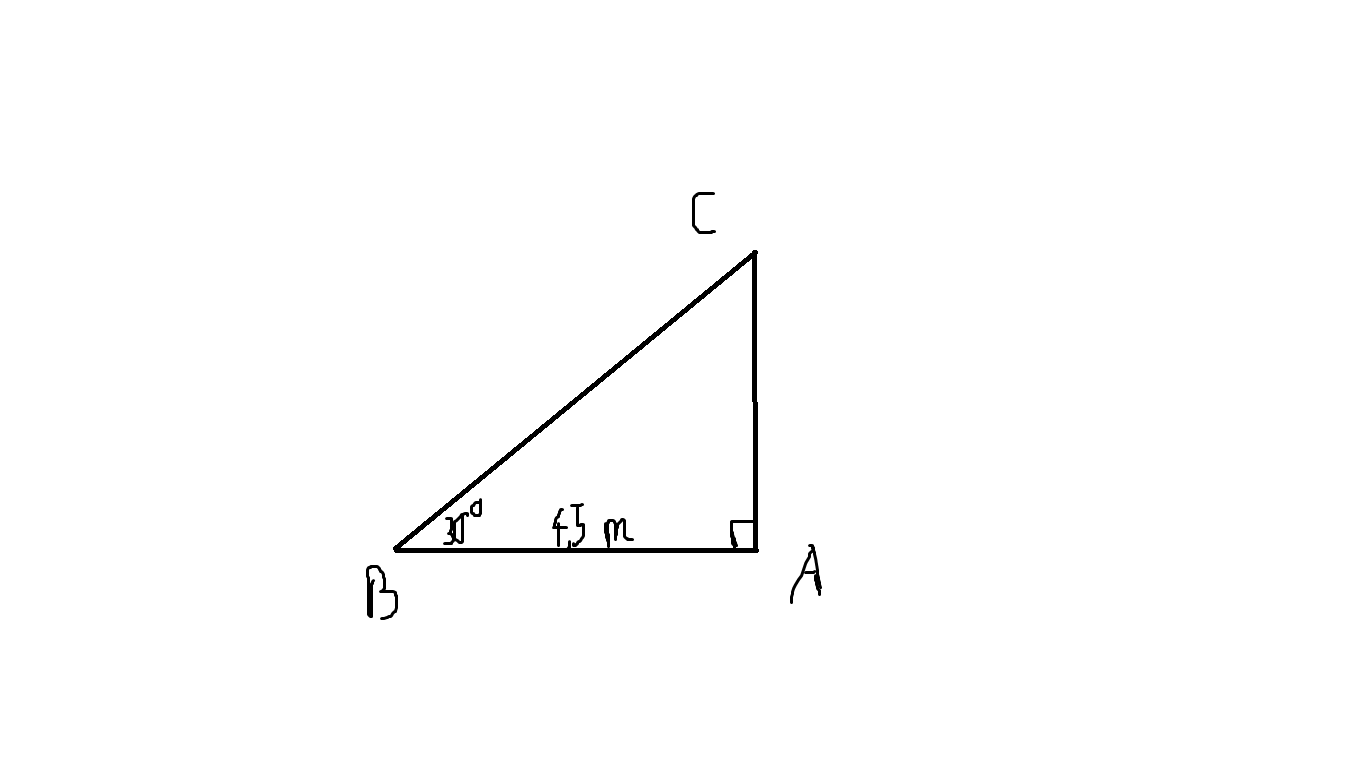
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)
Đúng 0
Bình luận (0)
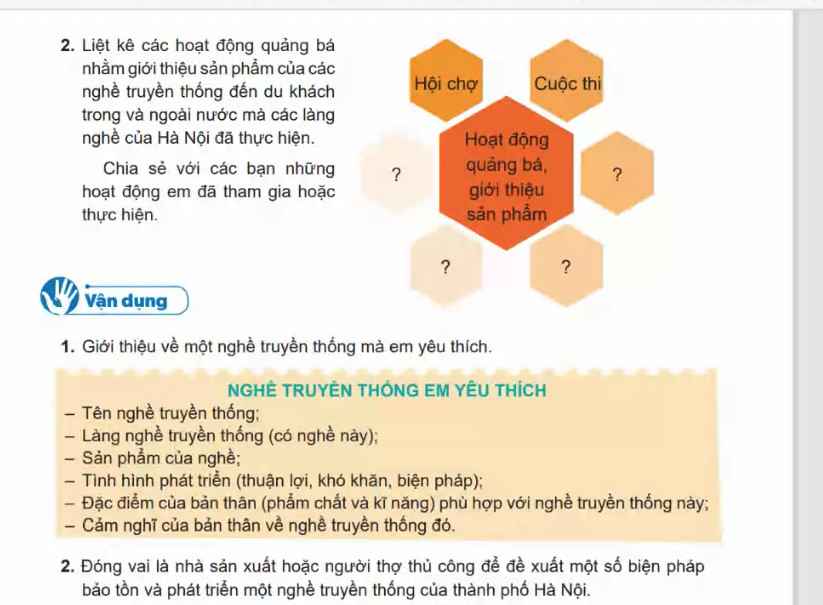
Mn giúp mik phần 1 2 nhé! Thanks

mn giải hộ mình câu 2 và câu 3 tự luận thui nhé
Mn giải giúp mik câu 2 và phần b câu 3 với ạ . Cảm ơn mn nhiều
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
Đúng 1
Bình luận (1)
Giúp m` cái mn ơi
1/1+2+1/1+2+3=1/2+3+4+....+1/1+2+3+....+50
Lưu ý / = phần của stp mn nhé
Mn giúp mk lm bài 2 SGK lớp 4 tập 1, ở phần Chính Tả nhé, mk đg cần gấp lắm, ai nhanh+ đúng thì mk tik cho nha
ơ hay!Phải nói rõ trang nào chứ
Trang 77 nha bn
Xem thêm câu trả lời
Các bạn làm nhanh lên nhé mình đang rất vội và đừng quên trả lời từng bước nhé ! (Phần 1)Câu 1) Tìm số a,b,c cho biết !1)dfrac{a}{5}dfrac{b}{4} và a^2-b^212)dfrac{a}{2}dfrac{b}{3}dfrac{c}{4} và a^2-b^2+c2^2108Câu 2) Tìm giá trị của các biểu thức sau ?1)3timesleft|1-2xright|-52)left(2^2x^2+1right)^4-33)left|x-dfrac{1}{2}right|+left(y+2right)^2+11(Lưu ý : Đoạn này các bạn sẽ bị mỏi tay đấy)Câu 3) Tính số học sinh của các lớp 7a và 7b .Biết lớp 7a ít hơn 7b là 5 học sinh và tỉ số học sinh của hai...
Đọc tiếp
Các bạn làm nhanh lên nhé mình đang rất vội và đừng quên trả lời từng bước nhé ! (Phần 1)
Câu 1) Tìm số a,b,c cho biết !
1)\(\dfrac{a}{5}=\dfrac{b}{4}\) và \(a^2-b^2=1\)
2)\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{4}\) và \(a^2-b^2+c2^2\)=108
Câu 2) Tìm giá trị của các biểu thức sau ?
1)\(3\times\left|1-2x\right|-5\)
2)\(\left(2^2x^2+1\right)^4-3\)
3)\(\left|x-\dfrac{1}{2}\right|+\left(y+2\right)^2+11\)
(Lưu ý : Đoạn này các bạn sẽ bị mỏi tay đấy)
Câu 3) Tính số học sinh của các lớp 7a và 7b .Biết lớp 7a ít hơn 7b là 5 học sinh và tỉ số học sinh của hai lớp là 8;9.
Câu 4) Hưởng ứng phong trò nhỏ của liên đội,ba chi đội 6a,6b,6c đã thu được tổng 120kg giấy vụn.Biết rằng số giấy vụn thu được của ba chi đội lần lượt tỉ lệ với 9;7;8.Hãy tính số giấy vụn thu được của các chi đội thu được ?
Câu 5) Cho biết hai đại lượng x và y tỉ lệ thuận với nhau và khi x = -6 thì y = 3.
A) Tìm hệ số tỉ lệ y đối với x
B) Hãy biểu diễn y theo x và biểu diễn x theo y
C) Tính giá trị của y theo x = \(\dfrac{1}{2}\)
D) Tính giá trị của x khi y = -8
còn tiếp ➜
Câu 5:
a: Hệ số tỉ lệ k của y đối với x là:
\(k=\dfrac{y}{x}=\dfrac{3}{-6}=-\dfrac{1}{2}\)
b: \(\dfrac{y}{x}=-\dfrac{1}{2}\)
=>\(y=-\dfrac{1}{2}x\)
=>\(x=\dfrac{\left(-2\right)\cdot y}{1}=-2y\)
c: Khi x=1/2 thì \(y=-\dfrac{1}{2}\cdot\dfrac{1}{2}=-\dfrac{1}{4}\)
d: Khi y=-8 thì \(x=\left(-2\right)\cdot\left(-8\right)=16\)
Câu 3:
Gọi số học sinh của hai lớp 7A và 7B lần lượt là a(bạn) và b(bạn)
(Điều kiện: \(a,b\in Z^+\))
Lớp 7A có ít hơn lớp 7B là 5 bạn nên b-a=5
Số học sinh của lớp 7A và lớp 7B lần lượt tỉ lệ với 8 và 9 nên ta có
\(\dfrac{a}{8}=\dfrac{b}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{8}=\dfrac{b}{9}=\dfrac{b-a}{9-8}=\dfrac{5}{1}=5\)
=>\(a=5\cdot8=40;b=5\cdot9=45\)
Vậy: Lớp 7A có 40 bạn; lớp 7B có 45 bạn
Câu 4:
Gọi khối lượng giấy vụn lớp 6a,6b,6c quyên góp được lần lượt là a(kg),b(kg),c(kg)
(Điều kiện: a>0;b>0;c>0)
Vì khối lượng giấy vụn mà ba lớp 6a,6b,6c quyên góp được lần lượt tỉ lệ với 9;7;8 nên \(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}\)
Tổng khối lượng giấy vụn ba lớp quyên góp được là 120kg nên a+b+c=120
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{9}=\dfrac{b}{7}=\dfrac{c}{8}=\dfrac{a+b+c}{9+7+8}=\dfrac{120}{24}=5\)
=>\(a=5\cdot9=45;b=5\cdot7=35;c=8\cdot5=40\)
Vậy: Lớp 6a quyên góp được 45kg; lớp 6b quyên góp được 35kg; lớp 6c quyên góp được 40kg
Đúng 2
Bình luận (0)
hỏi 1 câu cho vui vẻ kk nhé mn
thảm gì con người không dám bước lên? hack não nha. ai chả lời được sẽ được mik cho tick và kết bạn nhé^^[không cần kết bạn thì bảo luôn trong phần trả lời nhé:3
sai rồi bn kết bạn vs mik rồi để biết kết quả nha^^
thảm họa đúng ko
Xem thêm câu trả lời



