Đường tròn đường kính AB với A(3;-1), B(1;-5) có phương trình là gì?
PL
Những câu hỏi liên quan
Cho đoạn thẳng AB và 1 điểm C trên AB với ACa, BCb. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn đường kính AB tại P. Dựng đường tròn tâm P bán kính r1, tiếp xúc với CA,CD và tiếp xúc với nửa đường tròn đường kính AB. Dựng đường tròn tâm Q bán kính r2 tiếp xúc với CB,CD và tiếp xúc với nửa đường tròn đường kính AB. Gọi r là bán kính đường tròn nội tiếp tam giác ABDa/ Tính r1,r2 theo a,bb/Tìm đẳng thức liên hệ giữa r,r1,r2
Đọc tiếp
Cho đoạn thẳng AB và 1 điểm C trên AB với AC=a, BC=b. Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn đường kính AB tại P. Dựng đường tròn tâm P bán kính r1, tiếp xúc với CA,CD và tiếp xúc với nửa đường tròn đường kính AB. Dựng đường tròn tâm Q bán kính r2 tiếp xúc với CB,CD và tiếp xúc với nửa đường tròn đường kính AB. Gọi r là bán kính đường tròn nội tiếp tam giác ABD
a/ Tính r1,r2 theo a,b
b/Tìm đẳng thức liên hệ giữa r,r1,r2
Vẽ hình liên tiếp theo các cách diễn đạt sau:a. Vẽ đoạn thẳng AB2cm. Vẽ đường tròn (C1) tâm A , bán kính ABb. Vẽ đường tròn (C2) tâm B bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.c. Vẽ đường tròn (C3) tâm C, bán kính AC. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là Dd. Vẽ đường tròn (C4) tâm D bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là Ee. Vẽ đường tròn (C5) tâm E bán kính AE. Gọi giao điểm mới của đường tròn này...
Đọc tiếp
Vẽ hình liên tiếp theo các cách diễn đạt sau:
a. Vẽ đoạn thẳng AB=2cm. Vẽ đường tròn (C1) tâm A , bán kính AB
b. Vẽ đường tròn (C2) tâm B bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (C1) là C và G.
c. Vẽ đường tròn (C3) tâm C, bán kính AC. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là D
d. Vẽ đường tròn (C4) tâm D bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là E
e. Vẽ đường tròn (C5) tâm E bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (C1) là F
f. Vẽ đường tròn (C6) tâm F bán kính AF
g. Vẽ đường tròn (C7) tâm G bán kính AG
Sau khi vẽ như trên hãy so sánh các đoạn thẳng AB, BC, CD, DE, EF, FG, GB
Sau khi vẽ ta được hình như sau:
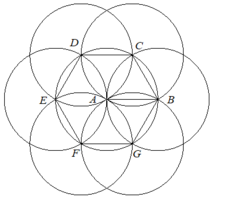
Khi đó, các đoạn thẳng A B = B C = C D = D E = E F = F G = G B (vì cùng bằng bán kính).
Đúng 0
Bình luận (0)
Trong nửa đường tròn tâm O đường kính AB =2R, đường tròn (I) tiếp xúc với nửa đường tròn (O) và đường kính AB. Đường tròn (K) tiếp xúc với nửa đường tròn (O) , đường tròn (I) và đường kính AB. Tính hiệu diện tích giữa đường tròn tâm I và đường tròn tâm K theo R
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D. Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E. Chứng minh CD song song với AB.

∆ ACB nội tiếp trong đường tròn (O) có AB là đường kính nên ∆ ABC vuông tại C
CO = OA = (1/2)AB (tính chất tam giác vuông)
AC = AO (bán kính đường tròn (A))
Suy ra: AC = AO = OC
∆ ACO đều góc AOC = 60 °
∆ ADB nội tiếp trong đường tròn đường kính AB nên ∆ ADB vuông tại D
DO = OB = OA = (1/2)AB (tính chất tam giác vuông)
BD = BO(bán kính đường tròn (B))
Suy ra: BO = OD = BD
∆ BOD đều

Đúng 0
Bình luận (0)
Cho đường tròn (O) và một điểm A trên đường tròn đó. Trên đoạn OA lấy điểm B sao cho OB 1/3 OA. Vẽ đường tròn đường kính AB.a) Chứng minh đường tròn đường kính AB tiếp xúc với đường tròn (O) cho trước.b) Vẽ đường tròn đồng tâm (O) với đường tròn (O) cho trước, căt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đồng tâm tại D và E ( D nằm giữa C và E). Chứng minh ACCDDE
Đọc tiếp
Cho đường tròn (O) và một điểm A trên đường tròn đó. Trên đoạn OA lấy điểm B sao cho OB= 1/3 OA. Vẽ đường tròn đường kính AB.
a) Chứng minh đường tròn đường kính AB tiếp xúc với đường tròn (O) cho trước.
b) Vẽ đường tròn đồng tâm (O) với đường tròn (O) cho trước, căt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đồng tâm tại D và E ( D nằm giữa C và E). Chứng minh AC=CD=DE
Ai giúp mình với mình nợ bài này lâu quá r
Đúng 0
Bình luận (0)
a) Gọi d là tiếp tuyến tại A của đường tròn (O) => d vuông góc OA => d vuông góc AB
Vì AB là đường kính của đường tròn (AB) nên d cũng là tiếp tuyến của (AB)
Vậy (O) và (AB) tiếp xúc nhau tại A (đpcm).
b) Gọi I là trung điểm đoạn AB => I là tâm của (AB) => ^ICA = ^IAC = ^OEA => IC // OE
Ta thấy OB = BI = IA = OA/3 => \(\frac{AI}{AO}=\frac{1}{3}\). Áp dụng ĐL Thales vào \(\Delta\)AEO có
\(\frac{AC}{AE}=\frac{AI}{AO}=\frac{1}{3}\) => AC = 1/3.AE (1)
Gọi OC,OD cắt đường tròn (O) cho trước lần lượt tại F,G. Khi đó DC // GF
Hay GF // AE. Mà GF và AE là các dây của đường tròn (O) nên (GE = (AF => ^EOG = ^AOF
Xét \(\Delta\)ODE và \(\Delta\)OCA: OD = OC, ^EOD = ^AOC (cmt), OE = OA => \(\Delta\)ODE = \(\Delta\)OCA (c.g.c)
=> ED = AC. Kết hợp với (1) suy ra AC = DE = AE/3 => AC = CD = DE (đpcm).
Đúng 0
Bình luận (0)
Vẽ hình liên tiếp theo cách diễn đạt sauVẽ đoạn thẳng AB 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB.Vẽ đường tròn (c2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là C và G.Vẽ đường tròn (c3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (c1) là D.Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (...
Đọc tiếp
Vẽ hình liên tiếp theo cách diễn đạt sau
Vẽ đoạn thẳng AB = 2cm. Vẽ đường tròn (c1) tâm A, bán kính AB.
Vẽ đường tròn (c2) tâm B, bán kính AB. Gọi các giao điểm của đường tròn này với đường tròn (c1) là C và G.
Vẽ đường tròn (c3) tâm C, bán kính AC. Goi giao điểm mới củađường tròn này với đường tròn (c1) là D.
Vẽ đường tròn (c4) tâm D, bán kính AD. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là E.
Vẽ đường tròn (c5) tâm E, bán kính AE. Gọi giao điểm mới của đường tròn này với đường tròn (c1) là F
Vẽ đường tròn (c6) tâm F, bán kính AF.
Vẽ đường tròn (c7) tâm G, bán kính AG.
Sau khi vẽ như trên hãy so sánh các đoạn thẳng: AB, BC, CD, DE, EF, FG, GB
Sau khi vẽ ta được hình bs.17
Khi đó, các đoạn thẳng: AB, BC, CD, EF, FG, GB bằng nhau (vì cùng bằng bán kính).
Đúng 0
Bình luận (0)
Cho ba điểm A,B,C thẳng hàng. Vẽ các đường tròn đường kính AB và AC. Gọi D là giao điểm của đường tròn đường kính AC với đường vuông góc với AC tại B. Từ C kể tiếp tuyến CK với đường tròn đường kính AB. Chứng minh CD=CK
Cho nửa đường tròn tâm O, đường kính AB. Lấy OA làm đường kính, vẽ nửa đường tròn nằm trên nửa mặt phẳng bờ AB chứa nửa đường tròn tâm O. Trên nửa đường tròn đường kính OA lấy điểm C không trùng với A và O, tia OC cắt nửa đường tròn tâm O tại D. Vẽ DH vuông góc với AB. CHứng minh AHCD là hình thang cân
Bài 2: Cho hình tròn tâm O, đường kính AB 8cm. a) Tính chu vi hình tròn tâm O, đường kính AB; hình tròn tâm M, đường kính OA và hình tròn tâm N, đường kính OB.b) So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.các bạn vẽ hình giúp mình
Đọc tiếp
Bài 2: Cho hình tròn tâm O, đường kính AB = 8cm.
a) Tính chu vi hình tròn tâm O, đường kính AB; hình tròn tâm M, đường kính OA và hình tròn tâm N, đường kính OB.
b) So sánh tổng chu vi của hình tròn tâm M và hình tròn tâm N với chu vi hình tròn tâm O.
các bạn vẽ hình giúp mình
a: CO=8*3,14=25,12(cm)
\(C_M=OA\cdot3.14=12.56\left(cm\right)\)
\(C_N=OB\cdot3.14=12.56\left(cm\right)\)
b: \(C_M+C_N=C_O\)
Đúng 0
Bình luận (1)
1) Cho đường tròn tâm O đường kính AB. Từ A và B vẽ 2 dây AC và BD cắt nhau tại N. 2 tiếp tuyến Cx, Dy của đường tròn cắt nhau tại M. P là giao điểm 2 đường thẳng AD và BC. Chứng minh:a) PN⊥ABb) P, M, N thẳng hàng.2) Cho tam giác ABC vuông ở A, đường cao AH. Đường tròn đường kính AH cắt AB, AC lần lượt tại E và F.Chứng minh EF^3EB.BC.CF3) Cho nửa đường tròn đường kính AB và tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ M trên Ax kẻ tiếp tuyến thứ 2 MC với nửa đường tròn, kẻ CH vuông...
Đọc tiếp
1) Cho đường tròn tâm O đường kính AB. Từ A và B vẽ 2 dây AC và BD cắt nhau tại N. 2 tiếp tuyến Cx, Dy của đường tròn cắt nhau tại M. P là giao điểm 2 đường thẳng AD và BC. Chứng minh:
a) \(PN⊥AB\)
b) P, M, N thẳng hàng.
2) Cho tam giác ABC vuông ở A, đường cao AH. Đường tròn đường kính AH cắt AB, AC lần lượt tại E và F.
Chứng minh \(EF^3=EB.BC.CF\)
3) Cho nửa đường tròn đường kính AB và tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ M trên Ax kẻ tiếp tuyến thứ 2 MC với nửa đường tròn, kẻ CH vuông góc với AB. CMR: MB đi qua trung điểm CH.


