Cho f(x)=ax2 +bx+c
Chứng minh rằng f(x)=0 có 2 nghiệm x1, x2 thỏa x1 <delta<x2 <=>a.f(x)<0
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
3x2 + 8x + 2
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Chứng tỏ rằng nếu phương trình a x 2 + b x + c = 0 có nghiệm là x 1 v à x 2 thì tam thức a x 2 + b x + c phân tích được thành nhân tử như sau:
a x 2 + b x + c = a ( x - x 1 ) ( x - x 2 )
Áp dụng : phân tích đa thức thành nhân tử.
a ) 2 x 2 - 5 x + 3 ; b ) 3 x 2 + 8 x + 2
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:

Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
2x2 - 5x + 3
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 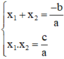
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 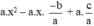
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 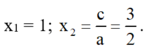
Vậy: 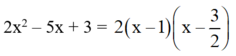
Cho tam thức bậc hai f ( x ) = a x 2 + b x + c có hai nghiệm thực phân biệt x 1 , x 2 Tính tích phân ∫ x 1 x 2 ( 2 a x + b ) 3 . e a x 2 + b x + c d x
![]()
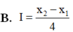
![]()
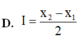
cho đa thức f(x) = x3 +ax2+bx-2
Xác định hệ số a,b biết đa thức có 2 nghiệm x1= -1; x2 = 1
Giải giúp mình với! Mình đang cần gấp !!!!!!! :3
làm ơn, mình đang cần rất gấp !!!!!!!!!!!!!
:((((((((((
Do x = -1 là nghiệm của phương trình
⇒ a - b - 1 - 2 = 0
⇒ a - b = 3
Tương tự ta có a + b = 1
Vậy a = 2 ; b = -1
1) đa thức f(x)=x^6-x^3+x^2-x+1 có hay ko có nghiệm trên tập hợp số thưc r
2)cho hàm số f(x) xác định với mọi x khác thỏa mãn : f(1)=1 và f(x1 +x2)=f(x1)+f (x2)với mọi x1,x2 jkhacs 0 , x1 + x2 cũng khác 0 và f (1/x)=1/x^2 . f(x) . CMR : f)5/7)=5/7
Cho đa thức: f(x) = x3 + ax2 + bx – 2
Xác định a, b biết đa thức có 2 nghiệm là x1 = -1 và x2 = 1.
Chứng minh rằng nếu đa thức f(x)=ax2+bx+c thỏa mãn f(2)=f(-3)=156 và f(-1)=132 thì đa thức f(x) ko có nghiệm.
Cho đa thức f(x) = ax^2 + bx + c
chứng tỏ rằng a+b +c =0 thì đa thức f(x) có 1 nghiệm = 1
b áp dụng tìm 1 nghiệm của đa thức f(x) = 5x^2 -6x +1
a: f(1)=0
=>a+b+c=0(luôn đúng)
b: f(x)=0
=>5x^2-6x+1=0
=>(x-1)(5x-1)=0
=>x=1/5 hoặc x=1