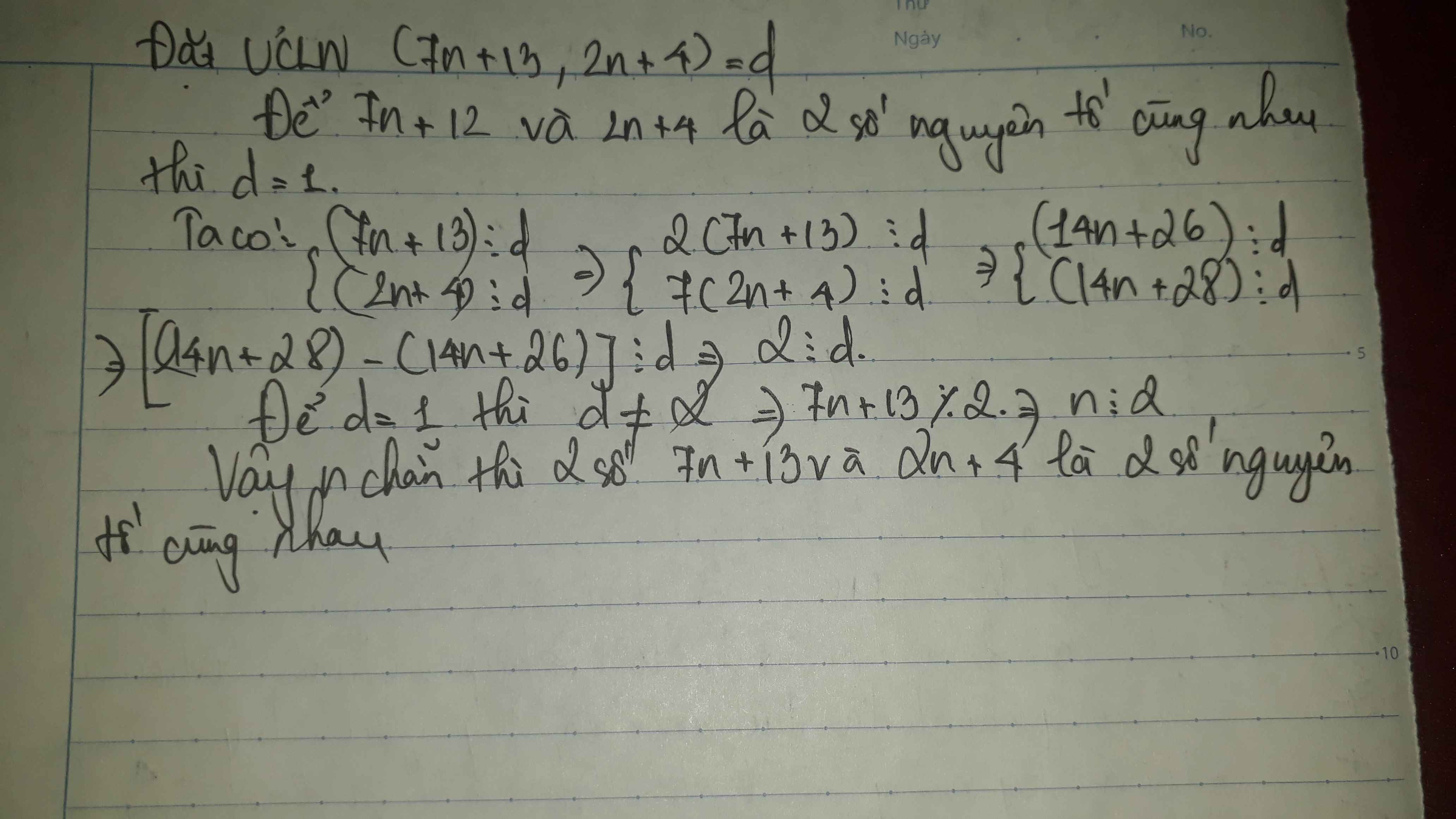tìm số tự nhiên n sao cho n+ 13 và n -2 là hai số nguyên tố cùng nhau
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
DL
Những câu hỏi liên quan
Tìm số tự nhiên n sao cho 7n+13 và 2n+4 là số nguyên tố cùng nhau
Vì 7n+13 và 2n+4 nguyên tố cùng nhau nên ta gọi d = UCLN(7n+13,2n+4)
=>7n+13 ⋮ d và 2n+4 ⋮ d
Có 7n+13 ⋮ d => 2(7n+13) ⋮ d => 14n+26 ⋮ d
2n+4 ⋮ d => 7.(2n+14) ⋮ d => 14n+28 ⋮ d
Suy ra (14n+28) – (14n+26) ⋮ d => 2 ⋮ d => d ∈ {1;2}
Nếu d = 1 thì 7n+13 và 2n+4 là nguyên tố cùng nhau
Nếu d = 2 => 7n+13 ⋮ 2 => 7.(n+1)+6 ⋮ 2 vì 6 ⋮ 2 nên 7.(n+1) ⋮ 2 mà UC(7,2) = 1 => n+1 ⋮ 2
Để n+1 ⋮ 2 thì n = 2k+1
Vậy để 7n+13 và 2n+4 là số nguyên tố cùng nhau thì n ≠ 2k+1
Đúng 0
Bình luận (0)
Tìm số tự nhiên n sao cho 7n + 13 và 2n + 4 là số nguyên tố cùng nhau
tìm số tự nhiên n sao cho :
7n+13 và 2n+4 là 2 số nguyên tố cùng nhau
Gọi ƯC(7n+13,2n+4)=d
Ta có: 7n+13 chia hết cho d=>2.(7n+13) chia hết cho d=>14n+26 chia hết cho d
2n+4 chia hết cho d=>7.(2n+4) chia hết cho d=>14n+28 chia hết cho d
=>14n+28-(14n+26) chia hết cho d
=>2 chia hết cho d
=>d=Ư(2)={1,2}
Để 7n+13 và 2n+4 à số nguyên tố cùng nhau
=>ƯC(7n+13,2n+4)=1
=>d=1
=>d khác 2
=>7n+13 không chia hết cho 2
mà 13 không chia hết cho 2
=>7n chia hết cho 2
Vì (2,7)=1
=>n chia hết cho 2
=>n=2k
Vậy n=2k
Đúng 0
Bình luận (0)
a, Tìm số tự nhiên n sao cho(4-n)chia hết cho (n+1)
b, Chứng tỏ rằng với mọi số tự nhiên n thì tích (n+3)×(n+6) chia hết cho 2
c, Cho a, b là hai số nguyên tố cùng nhau. Chứng minh rằng a và a+b cũng là 2 số nguyên tố cùng nhau
1.
$4-n\vdots n+1$
$\Rightarrow 5-(n+1)\vdots n+1$
$\Rightarrow 5\vdots n+1$
$\Rightarrow n+1\in \left\{1; 5\right\}$
$\Rightarrow n\in \left\{0; 4\right\}$
Đúng 0
Bình luận (0)
2.
Nếu $n$ chẵn $\Rightarrow n+6$ chẵn.
$\Rightarrow (n+3)(n+6)$ chẵn $\Rightarrow (n+3)(n+6)\vdots 2$
Nếu $n$ lẻ $\Rightarrow n+3$ chẵn.
$\Rightarrow (n+3)(n+6)$ chẵn $\Rightarrow (n+3)(n+6)\vdots 2$
Đúng 0
Bình luận (0)
3.
Giả sử $a,a+b$ không phải 2 số nguyên tố cùng nhau. Khi đó, đặt $d=ƯCLN(a,a+b)$. Điều kiện: $d\geq 2$.
$\Rightarrow a\vdots d; a+b\vdots d$
$\Rightarrow (a+b)-a\vdots d$
$\Rightarrow b\vdots d$
Vậy $a\vdots d; b\vdots d\Rightarrow d=ƯC(a,b)$. Mà $d\geq 2$ nên $a,b$ không phải 2 số nguyên tố cùng nhau (trái với đề bài)
Vậy điều giả sử là sai. Tức là $a,a+b$ là 2 số nguyên tố cùng nhau.
Đúng 0
Bình luận (0)
1. Chứng tỏ rằng với n \(\in\)N thìn+1 và 7n+4 là hai số nguyên tố cùng nhau.
2. Tìm n\(\in\)N thì 2n+1 và 4n+1 là hai số nguyên tố cùng nhau.
3. Tìm số nguyên tố p sao cho p+2 và p+4 đều là số nguyên tố.
4. Tìm số tự nhiên n sao cho \(n^2\)+3 là số chính phương.
tìm số tự nhiên n để hai số : 7n+ 13 và 2n+4 là hai số nguyên tố cùng nhau
a/ Tìm số tự nhiên n > 1 sao cho:
n + 8 chia hết cho n + 2
b/ Tìm số tự nhiên n để hai số sau nguyên tố cùng nhau:
9n + 11 và 12n + 15
a: \(\Leftrightarrow n+2=6\)
hay n=4
Đúng 0
Bình luận (0)
a) \(\left(n+2\right)+6⋮\left(n+2\right)\Rightarrow\left(n+2\right)\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
Do \(n\in\) N*, n>1 \(\Rightarrow n\in\left\{4\right\}\)
b) Gọi d là \(UCLN\left(9n+11;12n+15\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\left(9n+11\right)⋮d\\\left(12n+15\right)⋮d\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(36n+44\right)⋮d\\\left(36n+45\right)⋮d\end{matrix}\right.\)
\(\Rightarrow\left(36n+45\right)-\left(36n+44\right)⋮d\Rightarrow1⋮d\Rightarrowđpcm\)
Vậy 2 số trên luôn là 2 số nguyên tố cùng nhau
Đúng 0
Bình luận (0)
Tìm số tự nhiên n sao cho 4n+6 và 6n-5 là hai số nguyên tố cùng nhau
Cho n là số tự nhiên. Chứng minh 2n + 3 và n + 1 là hai số nguyên tố cùng nhau.
Cho n là số tự nhiên. Chứng minh n + 3 và n là hai số nguyên tố cùng nhau với n > 4.
Ai nhanh nhất mình tick cho
gọi d là ƯCLN(2n+3;n+1)
Ta có:n+1 chia hết cho d =>2n+2chia hết cho d(1)
2n+3 chia hết cho d(2)
Từ (1)(2)=>(2n+3)-(2n+2)chia hết cho d
hay 1 chia hết cho d
Vậy d=1=>2n+3 và n+1 là hai số nguyên tố cùng nhau(đpcm)
Đúng 1
Bình luận (0)
làm ơn làm phước cho mk 3 tick đi mk mà
please
Đúng 1
Bình luận (0)