Cho tam giác ABC có góc B=600; C=400.Lấy điểm D trên AC sao cho AD=AB, gọi M là trung điểm BD. Tia AM cắt BC tại K.
a) CMR: Tam giác AMB=AMD.
b) CMR: KB=KD.
c) Tính số đo góc DKC?
Cho lăng trụ tam giác ABC.A’B’C’ có đáy ABC là tam giác vuông tại C, BB’= a, góc B A C ^ = 60 0 , đường thẳng BB' tạo với (ABC) một góc 60 0 . Hình chiếu vuông góc của B' lên (ABC) trùng với trọng tâm của tam giác ABC. Thể tích V của khối tứ diện A’ .ABC là:
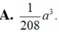
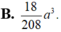
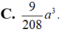
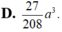
Chọn câu đúng nhất.1 .Cho ∆ ABC vuông cân tại A. vậy góc B bằng:A. 600B. 900C. 450D. 12002. Một tam giác là vuông nếu độ dài 3 cạnh của nó là:A. 2,3,4 B. 3,4,5 C. 4,5,6 D. 6,7,83. Một tam giác cân có góc ở đáy là 350 thì góc ở đỉnh có số đo là:A. 1000B. 1100C. 850D. 12004. Tam giác ABC có BC = 3cm ; AC = 5cm ; AB = 4cm. Tam giác ABC vuông tại đâu?A. Tại B B. Tại C C. Tại A D. Không phải là tam giác vuông5. Tam giác ABC có AB = AC = BC thì tam giác ABC là A. Tam giác nhọn B. Tam giác cân C. Tam giác vuông D. Tam giác đều6. Tam giác nào vuông nếu độ lớn ba góc kà:A. 300, 700, 800B. 200, 700, 900 C. 650, 450, 700D. 600, 600, 6007. Tam giác cân là tam giác có:A. Hai cạnh bằng nhau -B. Ba cạnh bằng nhau - C. Một góc bằng 600 - D. Một góc bằng 900
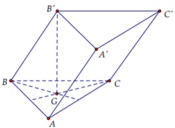
Cho hình lăng trụ tam giác ABC.A'B'C' có BB'=a, góc giữa đường thẳng BB' và mặt phẳng (ABC) bằng 60 0 , tam giác ABC vuông tại C và B A C ^ = 60 0 . Hình chiếu vuông góc của điểm B' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Thể tích của khối tứ diện A'.ABC tính theo a bằng
A. 9 a 3 416 .
B. 13 a 3 108 .
C. 9 a 3 208 .
D. 13 a 3 416 .
Câu 1 : Cho tam giác ABC có B - C = 30 độ . Tia phân giác của góc A cắt cạnh BC ở D. Tính góc ADB .
A. 300 B. 450 C. 600 D. 750
Câu 2 : Cho tam giác ABC ; A = 500 ; B : C = 2 : 3. Số đo các góc B và C lần lượt là:
A. 480 ; 820 B. 540 ; 760
C. 520 ; 780 D. 320 ; 880
CÁC BẠN GIẢI THÍCH CÁC BƯỚC SAO RA ĐƯƠC KẾT QUẢ GIÚP MIK VỚI NHA.
MIK CẢM ƠN NHIỀU NHA ^^
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại C, góc đường thẳng BB' tạo với (ABC) một góc 60 0 . Hình chiếu vuông góc của B' lên (ABC) trùng với trọng tâm của tam giác ABC. Thể tích V của khối tứ diện A'.ABC là
A. 1 208 a 3
B. 18 208 a 3
C. 9 208 a 3
D. 27 208 a 3
Bài 5: Cho tam giác ABC vuông tại A có góc B = 600, kẻ phân giác của góc B cắt AC tại D, lấy điểm M thuộc BC sao cho BM = AB.
a)Tam giác ABM là tam giác gì ?
b)Chứng minh: DM vuông góc với BC
a: Xét ΔBAM có BA=BM và góc ABM=60 độ
nên ΔBAM đều
b: Xét ΔBAD và ΔBMD có
BA=BM
góc ABD=góc MBD
BD chung
=>ΔBAD=ΔBMD
=>góc BMD=góc BAD=90 độ
=>DM vuông góc BC
Cho tam giác ABC vuông tại A có góc B = 600, AB = a Tính A C → . C B →
A. 3a2
B. -3a2
C. a2
D. -2a2
có ai bt giải bài này k giúp mk vs mk đg rất rất cần mong các bạn giúp cho
Bài 1:cho tam giác ABC có góc B= 600, góc C=500, AC=35cm. Tính diện tích tam giác ABC
Kẻ AH vuông góc với BC
Trong tam giác vuông AHC ta có:
cosC=HC/AC⇒HC=cosC.AC=cos50.35≈22cm
⇒AH=√AC^2−HC^2=√35^2−22^2=√741cm
Trong tam giác vuông AHB ta có:
sinB=AH/AB⇒AB=AH/sinB=√741/sin60=2√247cm
⇒HB=√AB^2−AH^2=√(2√247)^2−741=√247cm
Vậy SABC=AH(HB+HC)/2=√741.(√247+22)/2≈513\(cm^2\)
Cho tam giác ABC cân tại A có B = 400 . Cho AD là tia phân giác của góc BAC. Số đo góc DAB là
A, 600 B. 1000 C. 300 D. 500
có ai bt giải bài này k giúp mk vs mk đg rất rất cần mong các bạn giúp cho
Bài 1:cho tam giác ABC có góc B= 600, góc C=500, AC=35cm. Tính diện tích tam giác ABC
Bài 2 : cho tứ giác ABCD có góc A = góc D= 900, góc C=400, AB=4cm, AD=3cm. Tính diện tích tứ giác
mong các bn giúp cho
1.
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)
2.
Ta có \(A+D=180^0\Rightarrow AB||CD\) (hai góc trong cùng phía bù nhau)
\(\Rightarrow\) Tứ giác ABCD là hình thang vuông tại A và D
Từ B kẻ BE vuông góc CD \(\Rightarrow ABED\) là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow\left\{{}\begin{matrix}DE=AB=4\left(cm\right)\\BE=AD=3\left(cm\right)\end{matrix}\right.\)
Trong tam giác vuông BCE:
\(tanC=\dfrac{BE}{CE}\Rightarrow CE=\dfrac{BE}{tanC}=\dfrac{3}{tan40^0}\approx3,6\left(cm\right)\)
\(\Rightarrow CD=DE+CE=4+3,6=7,6\left(cm\right)\)
\(\Rightarrow S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.3.\left(4+7,6\right)=17,4\left(cm^2\right)\)