Đề bài yêu cầu gì vậy bạn?

Bài 3:

a, (\(x\)+y+z)²

=((\(x\)+y) +z)²

= (\(x\) + y)² + 2(\(x\) + y)z + z²

= \(x^2\) + 2\(xy\) + y² + 2\(xz\) + 2yz + z²

=\(x^2\) + y² + z² + 2\(xy\) + 2\(xz\) + 2yz

b, (\(x-y\))(\(x^2\) + y² + z² - \(xy\) - yz - \(xz\))

= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y³ 

Đến dây ta thấy xuất hiện \(x^3\) - y³ khác với đề bài, em xem lại đề bài nhé

c,

(\(x\) + y + z)³ 

=(\(x\) + y)³ + 3(\(x\) + y)²z + 3(\(x\)+y)z² + z³

= \(x^3\) + 3\(x^2\)y + 3\(xy^{2^{ }}\) + y³ +  3(\(x\)+y)z(\(x\) + y + z) + z³

= \(x^3\) + y³ + z³ + 3\(xy\)(\(x\) + y) + 3(\(x+y\))z(\(x+y+z\))

= \(x^3\) + y³ + z³ + 3(\(x\) + y)( \(xy\) + z\(x\) + yz + z²)

= \(x^3\) + y³ + z³ + 3(\(x\) + y){(\(xy+xz\)) + (yz + z²)}

= \(x^3\) + y³ + z³ + 3(\(x\) + y){ \(x\)( y +z) + z(y+z)}

= \(x^3\) + y³ + z³ + 3(\(x\) + y)(y+z)(\(x+z\)) (đpcm)

\(a,x+y=1\Leftrightarrow\left(x+y\right)^3=1\Leftrightarrow x^3+y^3+3xy\left(x+y\right)=1\\ \Leftrightarrow x^3+y^3+3xy\cdot1=1\Leftrightarrow x^3+y^3+3xy=1\)

\(b,x^3-y^3-3xy\\ =x^3-3x^2y+3xy^2-y^3-3xy+3x^2y-3xy^2\\ =\left(x-y\right)^3-3xy\left(x-y-1\right)\\ =1^3-3xy\left(1-1\right)=1-0=1\)

\(c,x^3+y^3+3xy\left(x^2+y^2\right)+6x^2y^2\left(x+y\right)\\ =\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\left[\left(x+y\right)^2-2xy\right]+6x^2y^2\\ =x^2-xy+y^2+3xy-6x^2y^2+6x^2y^2\\ =x^2+2xy+y^2=\left(x+y\right)^2=1\)

a: (x+y+z)^3-x^3-y^3-z^3

=(x+y+z-x)(x^2+2xy+y^2-x^2-xy-xz+z^2)-(y+z)(y^2-yz+z^2)

=(x+y)(y+z)(x+z)

b: x^3+y^3+z^3=1

x+y+z=1

=>x+y=1-z

x^3+y^3+z^3=1

=>(x+y)^3+z^3-3xy(x+y)=1

=>(1-z)^3+z^3-3xy(1-z)=1

=>1-3z-3z^2-z^3+z^3-3xy(1-z)=1

=>1-3z+3z^2-3xy(1-z)=1

=>-3z+3z^2-3xy(1-z)=0

=>-3z(1-z)-3xy(1-z)=0

=>(z-1)(z+xy)=0

=>z=1 và xy=0

=>z=1 và x=0; y=0

A=1+0+0=1

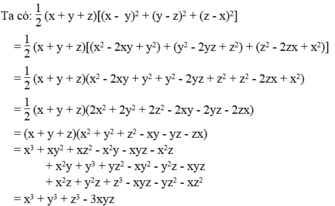
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Nếu x ≥ 0, y  ≥  0, z  ≥  0 thì:

x + y + z  ≥  0

x - y 2 + y - z 2 + z - x 2 ≥ 0

Suy ra:

x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z

Hay:  x 3 + y 3 + z 3 3 ≥ x y z

Áp dụng bđt AM - GM:

\(x^3+1+1\ge3x;y^3+1+1\ge3y;z^3+1+1\ge3z;2x+2y+2z\ge6\sqrt[3]{xyz}=6\).

Cộng vế với vế các bđt trên rồi rút gọn ta có đpcm.

Áp dụng BĐT Cosi:

\(\left(x^3+1+1\right)+\left(y^3+1+1\right)+\left(z^3+1+1\right)\)

\(\ge3\left(x+y+z\right)\)

\(\ge x+y+z+2.3\sqrt[3]{xyz}\)

\(=x+y+z+6\)

\(\Rightarrow x^3+y^3+z^3\ge x+y+z\)

Đẳng thức xảy ra khi \(x=y=z=1\)

\(x^3+y^3+z^3-3xyz=0\)

\(\Leftrightarrow\left(x+y\right)^3+z^3-3xy\left(x+y\right)-3xyz=0\)

\(\Leftrightarrow\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)=0\)

\(\Leftrightarrow x^2+y^2+z^2-xy-xz-yz=0\)

\(\Leftrightarrow x=y=z\)

Biến đổi tương đương nhé bạn.

a: Ta có: \(\left(x+y\right)^2\)

\(=x^2+2xy+y^2\)

\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)