M.n giúp em với ạ. Em càn gấp 🙏😭
C2
Những câu hỏi liên quan
Giúp em bài 5 với ạ. Cần gấp lắm. Em cảm ơn ạ 🙏🙏🙏🙏🙏😭😭
5:
a: sin x=2*cosx
\(A=\dfrac{6cosx+2cosx-4\cdot8\cdot cos^3x}{cos^3x-2cosx}\)
\(=\dfrac{8-32cos^2x}{cos^2x-2}\)
b: VT=sin^4(pi/2-x)+cos^4(x+pi/2)+6*1/2*sin^22x+1/2*cos4x
=cos^4x+sin^4x+3*sin^2(2x)+1/2*(1-2*sin^2(2x))
=1-2*sin^2x*cos^2x+3*sin^2(2x)+1/2-sin^2(2x)
==3/2=VP
Đúng 0
Bình luận (0)
Giúp em bài 1, 2 với. Cần gấp 🙏🙏🙏🙏😭
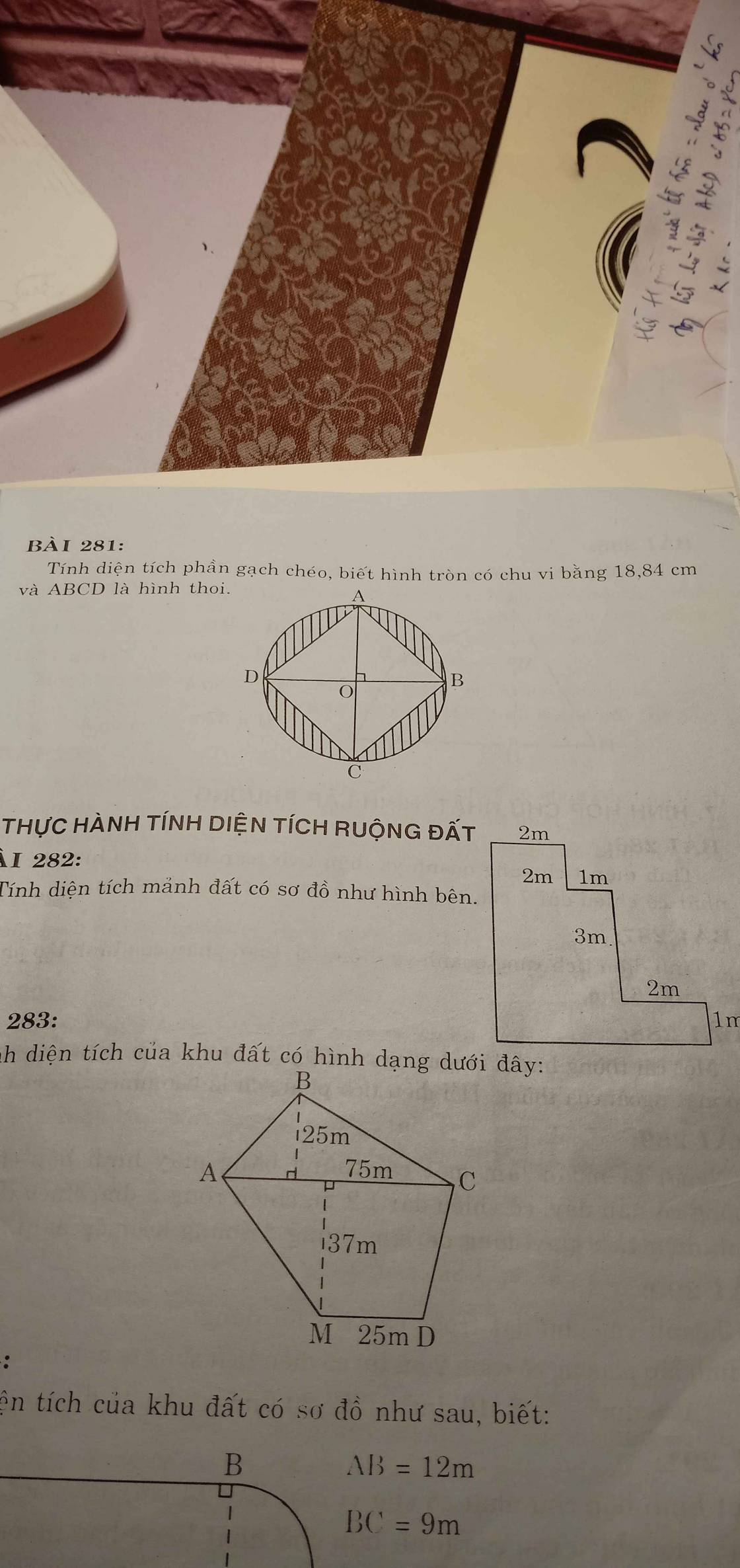 giúp em bài 281 với ạ,em cần gấp ạ🙏🙏🙏🙏🙏🙏
giúp em bài 281 với ạ,em cần gấp ạ🙏🙏🙏🙏🙏🙏
Bán kính hình tròn:
\(18,84:3,14:2=3\left(cm\right)\)
Diện tích hình tròn:
\(3\times3\times3,14=28,26\left(cm^2\right)\)
Đường kính hình tròn:
\(3\times2=6\left(cm\right)\)
Diện tích hình thoi:
\(\dfrac{6\times6}{2}=18\left(cm^2\right)\)
Diện tích phần gạch chéo:
\(28,26-18=10,26\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Mong m.n giúp em ạ 😭😭 , em c.ơn 
GIÚP EM VỚI Ạ,EM CÀN GẤP Ạ,LÀM CỤ THỂ GIÚP EM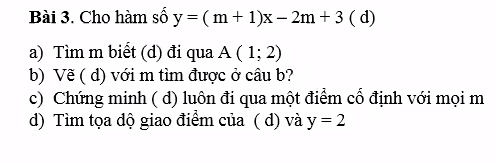
Giúp em bài 4 với ạ. Cần gấp gấp 🥺🥺🥺🥺🙏🙏🙏🙏🙏🙏🙏
4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)
Đúng 1
Bình luận (0)
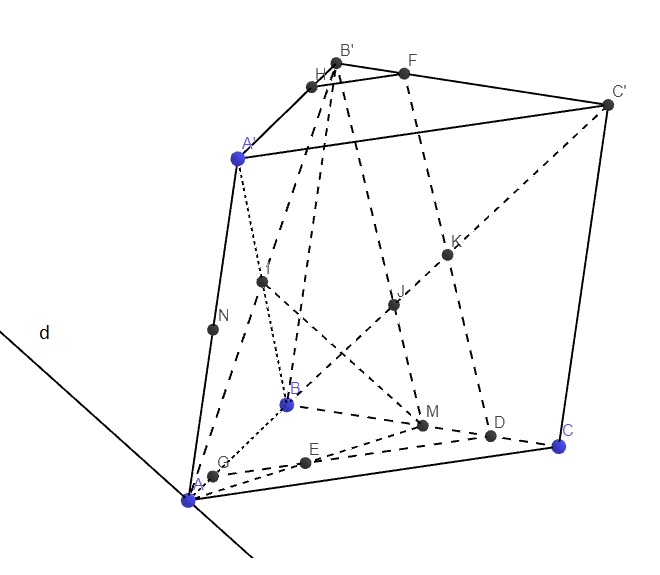
Giúp em câu 4 với ạ. Cần gấp lắm ạ😢😢🙏🙏🙏
a.
Trong tam giác A'BC ta có: I là trung điểm BA', M là trung điểm BC
\(\Rightarrow IM\) là đường trung bình tam giác A'BC
\(\Rightarrow IM||A'C\)
\(\Rightarrow IM||\left(ACC'A'\right)\)
Do \(A\in\left(AB'M\right)\cap\left(ACC'A'\right)\) và \(\left\{{}\begin{matrix}IM\in\left(AB'M\right)\\A'C\in\left(ACC'A'\right)\\IM||A'C\end{matrix}\right.\)
\(\Rightarrow\) Giao tuyến của (AB'M) và (ACC'A') là đường thẳng qua A và song song A'C
Qua A kẻ đường thẳng d song song A'C
\(\Rightarrow d=\left(AB'M\right)\cap\left(ACC'A'\right)\)
b.
I là trung điểm AB', E là trung điểm AM
\(\Rightarrow IE\) là đường trung bình tam giác AB'M \(\Rightarrow IE||B'M\) (1)
Tương tự ta có IN là đường trung bình tam giác AA'B' \(\Rightarrow IN||A'B'\) (2)
(1);(2) \(\Rightarrow\left(EIN\right)||\left(A'B'M\right)\)
Đúng 0
Bình luận (0)
c.
Trong mp (BCC'B'), qua K kẻ đường thẳng song song B'M lần lượt cắt BC và B'C' tại D và F
\(DF||B'M\Rightarrow DF||IE\Rightarrow DF\subset\left(EIK\right)\)
Trong mp (ABC), nối DE kéo dài cắt AB tại G
\(\Rightarrow G\in\left(EIK\right)\)
Trong mp (A'B'C'), qua F kẻ đường thẳng song song A'C' cắt A'B' tại H
Do IK là đường trung bình tam giác A'BC' \(\Rightarrow IK||A'B'\)
\(\Rightarrow FH||IK\Rightarrow H\in\left(EIK\right)\)
\(\Rightarrow\) Tứ giác DFHG là thiết diện (EIK) và lăng trụ
Gọi J là giao điểm BK và B'M \(\Rightarrow J\) là trọng tâm tam giác B'BC
\(\Rightarrow\dfrac{BJ}{BK}=\dfrac{2}{3}\)
Áp dụng talet: \(\dfrac{BM}{BD}=\dfrac{BJ}{BK}=\dfrac{2}{3}\Rightarrow BD=\dfrac{3}{2}BM=\dfrac{3}{2}.\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
\(\Rightarrow MD=\dfrac{1}{4}BC=\dfrac{1}{2}CM\Rightarrow D\) là trung điểm CM
\(\Rightarrow DE\) là đường trung bình tam giác ACM
\(\Rightarrow DE||AC\Rightarrow DE||FH\)
\(\Rightarrow\) Thiết diện là hình thang
Đúng 0
Bình luận (0)
Mọi người ơi giúp em với em đang gấp 🙏🙏
72 : (x -2)ᒾ = 8
75 - 5 (x-3)³ =700
Giúp em với ạ🙏🙏🙏
a/
\(\frac{72}{\left(x-2\right)^2}=8\left(x\ne2\right)\Rightarrow\left(x-2\right)^2=9=3^2\)
\(\Rightarrow\left|x-2\right|=3\)
+ Nếu \(x-2\ge0\Rightarrow x\ge2\Rightarrow x-2=3\Rightarrow x=5\) (thoả mãn đk \(x\ge2\) )
+ Nếu \(x-2< 0\Rightarrow x< 2\Rightarrow2-x=3\Rightarrow x=-1\) (Thoả mãn đk \(x< 2\) )
b/
\(75-5\left(x-3\right)^3=700\Rightarrow\left(x-3\right)^3=-125=\left(-5\right)^3\)
\(\Rightarrow x-3=-5\Rightarrow x=-2\)
Giúp em với ạ. Cần gấp 😥😥😥😥🙏🙏🙏🙏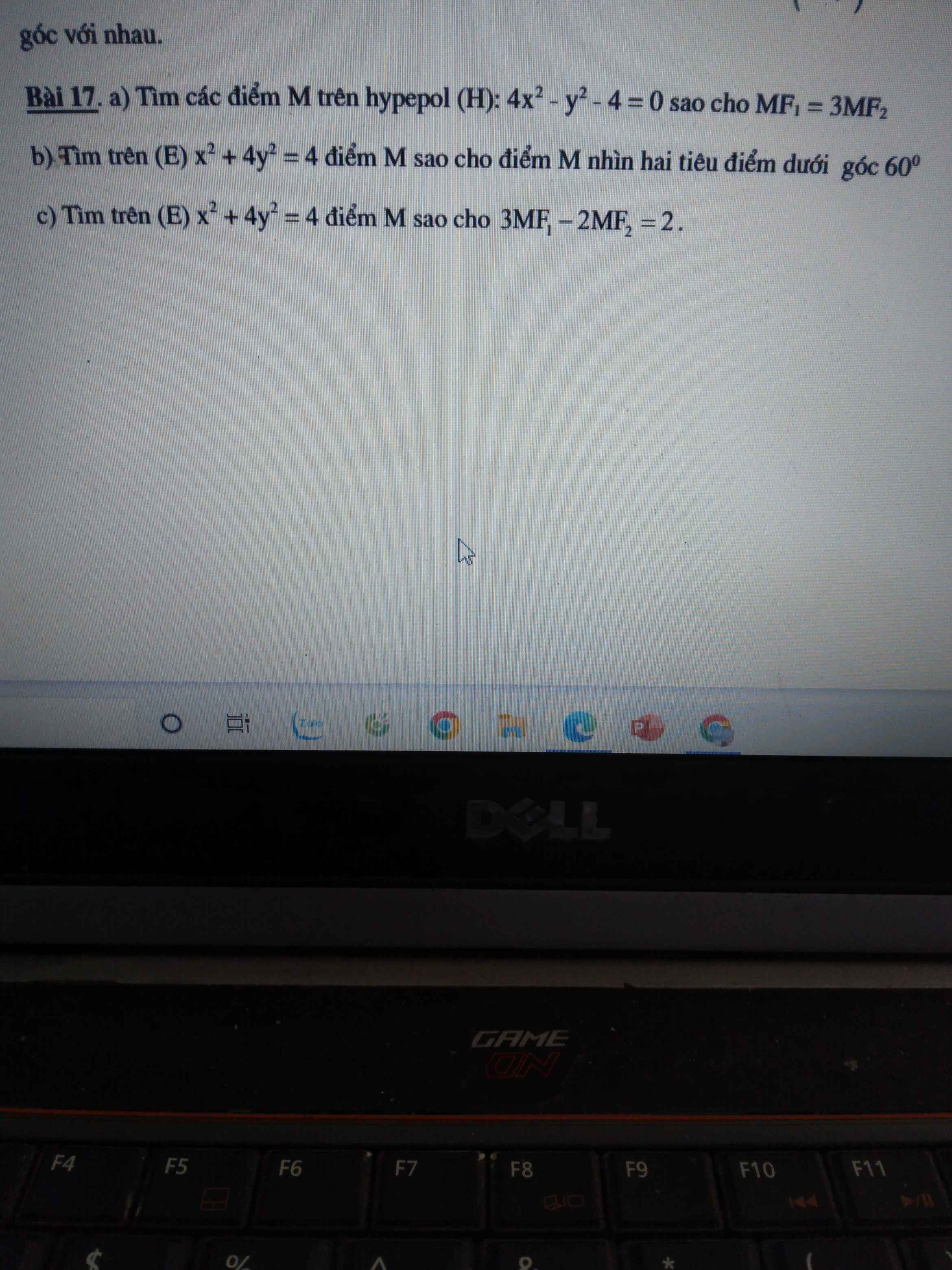
Ét O Ét, giúp em bài 4 với ạ 🙏🙏🙏🙏🙏. Cần gấp
4:
a: -90<a<0
=>cos a>0
cos^2a=1-(-4/5)^2=9/25
=>cosa=3/5
\(sin\left(45-a\right)=sin45\cdot cosa-cos45\cdot sina=\dfrac{\sqrt{2}}{2}\left(cosa-sina\right)\)
\(=\dfrac{\sqrt{2}}{2}\left(\dfrac{3}{5}-\dfrac{4}{5}\right)=\dfrac{-\sqrt{2}}{10}\)
b: pi/2<a<pi
=>cosa<0
cos^2a+sin^2a=0
=>cos^2a=16/25
=>cosa=-4/5
tan a=3/5:(-4/5)=-3/4
\(tan\left(a+\dfrac{pi}{3}\right)=\dfrac{tana+\dfrac{tanpi}{3}}{1-tana\cdot tan\left(\dfrac{pi}{3}\right)}\)
\(=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\dfrac{-3}{4}\cdot\sqrt{3}}=\dfrac{48-25\sqrt{3}}{11}\)
c: 3/2pi<a<pi
=>cosa>0
cos^2a+sin^2a=1
=>cos^2a=25/169
=>cosa=5/13
cos(pi/3-a)
\(=cos\left(\dfrac{pi}{3}\right)\cdot cosa+sin\left(\dfrac{pi}{3}\right)\cdot sina\)
\(=\dfrac{5}{13}\cdot\dfrac{1}{2}+\dfrac{-12}{13}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{5-12\sqrt{3}}{26}\)
Đúng 0
Bình luận (0)