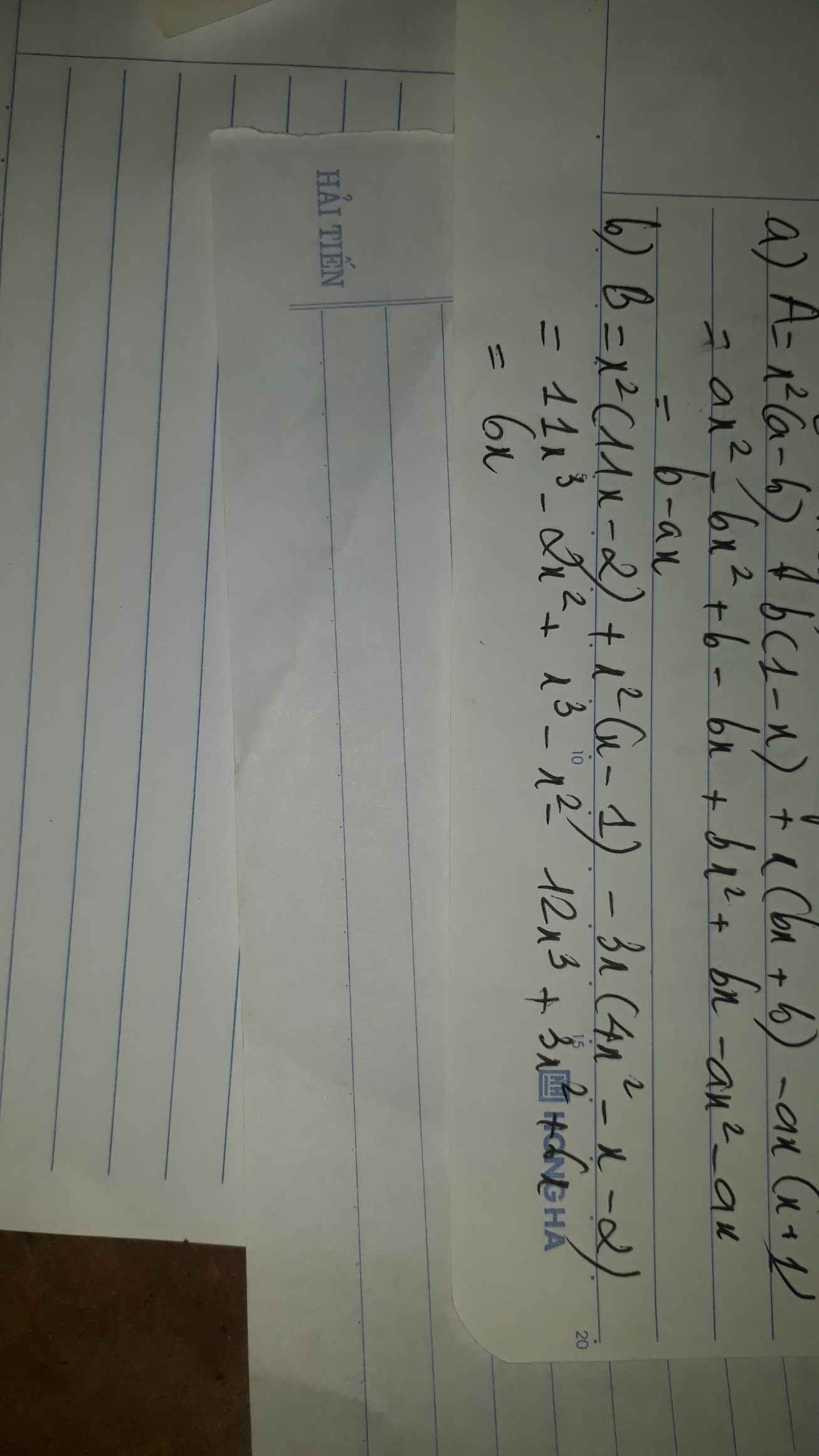Chứng minh rằng nếu 1 ≤ 𝑥 ≤ 3 thì 𝑥 2 + 3 ≤ 4𝑥. Khi nào xảy ra dấu bằng
OH
Những câu hỏi liên quan
1) (𝑥 + 7)2 − 𝑥(𝑥 − 3) = 15 2) (2𝑥 + 3)2 − 4𝑥(𝑥 + 2) = 13 3) (3 − 𝑥)2 − (𝑥 − 2)(𝑥 + 1) = 21 4) (𝑥 − 2)2 − (𝑥 + 1)(𝑥 + 3) = −7 5) (𝑥 + 3)(4 − 𝑥) + (𝑥 + 1)(𝑥 − 1) = 10 6) (𝑥 + 1)2 − (𝑥 − 2)(𝑥 + 2) = 13 7) (5𝑥 − 1)(5𝑥 + 1) = 25𝑥2 − 7𝑥 + 15 8) (2𝑥 − 3)2 = 4(𝑥 − 3)(𝑥 + 3) − 4 . Số 2 ở sau là mũ 2 nhé, giải giúp mình vs
???????????????????????
a. Chứng minh rằng ∀ 𝑎, 𝑏 > 0 thì 𝑎 2+𝑏 2 𝑎+𝑏 ≥ 𝑎+𝑏 2
b. Chứng minh rằng ∀ 𝑥, 𝑦, 𝑧 > 0 thì 𝑥 2 𝑥+𝑦 + 𝑦 2 𝑦+𝑧 + 𝑧 2 𝑧+𝑥 = 𝑦 2 𝑥+𝑦 + 𝑧 2 𝑦+𝑧 + 𝑥 2 𝑧+𝑥
c. Chứng minh rằng ∀ 𝑥, 𝑦, 𝑧 > 0 thì 𝑥 2 𝑥+𝑦 + 𝑦 2 𝑦+𝑧 + 𝑧 2 𝑧+𝑥 ≥ 𝑥+𝑦+
Rút gọn a) 𝐴 = 𝑥^ 2 (𝑎 − 𝑏) + 𝑏(1 − 𝑥) + 𝑥(𝑏𝑥 + 𝑏) − 𝑎𝑥(𝑥 + 1) b) 𝐵 = 𝑥 2 (11𝑥 − 2) + 𝑥 2 (𝑥 − 1) − 3𝑥(4𝑥 2 − 𝑥 − 2)
b: Ta có: \(B=x^2\left(11x-2\right)+x^2\left(x-1\right)-3x\left(4x^2-x-2\right)\)
\(=11x^3-2x^2+x^3-x^2-12x^3+3x^2+6x\)
\(=6x\)
Đúng 0
Bình luận (0)
Bài 2: Tìm x biết
1. (𝑥 − 3)² = 4𝑥 ²+ 20x + 25
2. 2x(x – 4) + 𝑥² – 16 = 0
Lời giải:
1.
$(x-3)^2=4x^2+20x+25=(2x+5)^2$
$\Leftrightarrow (x-3)^2-(2x+5)^2=0$
$\Leftrightarrow (x-3-2x-5)(x-3+2x+5)=0$
$\Leftrightarrow (-x-8)(3x+2)=0$
$\Leftrightarrow -x-8=0$ hoặc $3x+2=0$
$\Leftrightarrow x=-8$ hoặc $x=-\frac{2}{3}$
2.
$2x(x-4)+x^2-16=0$
$\Leftrightarrow 2x(x-4)+(x-4)(x+4)=0$
$\Leftrightarrow (x-4)(2x+x+4)=0$
$\Leftrightarrow (x-4)(3x+4)=0$
$\Leftrightarrow x-4=0$ hoặc $3x+4=0$
$\Leftrightarrow x=4$ hoặc $x=-\frac{4}{3}$
Đúng 1
Bình luận (0)
Bài 8: Tìm giá trị nhỏ nhất của
A=√𝑥2 −4𝑥+25 ,
C=3+√𝑥 √𝑥+1
B=√𝑥2 −6𝑥+30
D=√𝑥2 −4𝑥+7+√2
bạn viết câu hỏi dưới dạng trực quan để mn dễ hiểu nhé!
Đúng 0
Bình luận (0)
Tìm x , biết rằng
a) 𝑥3 - 64𝑥 0
b) 𝑥3 - 4𝑥2 -4𝑥
c)𝑥2 - 16 - (𝑥 - 4) 0
d)(2𝑥 + 1)2 (3 + 𝑥)
e)𝑥3 - 6𝑥2 + 12𝑥 - 8 0
f)𝑥3 - 7𝑥 - 6 0
Đọc tiếp
Tìm x , biết rằng
a) 𝑥3 - 64𝑥 = 0
b) 𝑥3 - 4𝑥2 = -4𝑥
c)𝑥2 - 16 - (𝑥 - 4) = 0
d)(2𝑥 + 1)2 = (3 + 𝑥)
e)𝑥3 - 6𝑥2 + 12𝑥 - 8 = 0
f)𝑥3 - 7𝑥 - 6 = 0
a) x³ - 64x = 0
x(x² - 64) = 0
x(x - 8)(x + 8) = 0
x = 0 hoặc x - 8 = 0 hoặc x + 8 = 0
*) x - 8 = 0
x = 8
*) x + 8 = 0
x = -8
Vậy x = -8; x = 0; x = 8
b) x³ - 4x² = -4x
x³ - 4x² + 4x = 0
x(x² - 4x + 4) = 0
x(x - 2)² = 0
x = 0 hoặc (x - 2)² = 0
*) (x - 2)² = 0
x - 2 = 0
x = 2
Vậy x = 0; x = 2
c) x² - 16 - (x - 4) = 0
(x - 4)(x + 4) - (x - 4) = 0
(x - 4)(x + 4 - 1) = 0
(x - 4)(x + 3) = 0
x - 4 = 0 hoặc x + 3 = 0
*) x - 4 = 0
x = 4
*) x + 3 = 0
x = -3
Vậy x = -3; x = 4
d) (2x + 1)² = (3 + x)²
(2x + 1)² - (3 + x)² = 0
(2x + 1 - 3 - x)(2x + 1 + 3 + x) = 0
(x - 2)(3x + 4) = 0
x - 2 = 0 hoặc 3x + 4 = 0
*) x - 2 = 0
x = 2
*) 3x + 4 = 0
3x = -4
x = -4/3
Vậy x = -4/3; x = 2
e) x³ - 6x² + 12x - 8 = 0
(x - 2)³ = 0
x - 2 = 0
x = 2
f) x³ - 7x - 6 = 0
x³ + 2x² - 2x² - 4x - 3x - 6 = 0
(x³ + 2x²) - (2x² + 4x) - (3x + 6) = 0
x²(x + 2) - 2x(x + 2) - 3(x + 2) = 0
(x + 2)(x² - 2x - 3) = 0
(x + 2)(x² + x - 3x - 3) = 0
(x + 2)[(x² + x) - (3x + 3)] = 0
(x + 2)[x(x + 1) - 3(x + 1)] = 0
(x + 2)(x + 1)(x - 3) = 0
x + 2 = 0 hoặc x + 1 = 0 hoặc x - 3 = 0
*) x + 2 = 0
x = -2
*) x + 1 = 0
x = -1
*) x - 3 = 0
x = 3
Vậy x = -1; x = -1; x = 3
Đúng 1
Bình luận (1)
a,x\(^3\)-64=0
x\(^3\) =64
=>x=3
b,x\(^3\)-4x\(^2\)=-4x
x\(^3\)-4x\(^2\)+4x=0
x(x\(^2\)-4x+4)=0
x(x-2)\(^2\)=)
TH1:x=0
TH2:x-2=0
=>x=2
c,x\(^2\)-16-(x-4)=0
(x+4)(x-4)-(x-4)=0
(x-4)(x+4-1)=0
(x-4)(x+3)=0
TH1:x-4=0
=>x=4
TH2:x+3=0
=>x=-3
d,(2x+1).2=3+x
4x+2-3-x=0
3x-1=0
x=\(\dfrac{1}{3}\)
e,x\(^3\)-6x\(^2\)+12x-8=0
(x-2)\(^3\)=0
=>x-2=0
=>x=2
f,x\(^3\)-7x+6=0
x\(^3\)-x-6x+6=0
x(x\(^2\)-1)-6(x-1)=0
x(x+1)(x-1)-6(x-1)=0
(x-1)(x\(^2\)+x-6)=0
TH1:x-1=0
=>x=1
TH2:x\(^2\)+x-6=0
x\(^2\)+3x-2x-6=0
x(x+3)-2(x+3)=0
(x+3)(x-2)=0
=>x+3=0 =>x-2=0
+>x=-3 =>x=2
Đúng 0
Bình luận (0)
d,(2x+1)\(^2\)=(3+x)\(^2\)
4x\(^2\)+4x+1-9-6x-x\(^2\)=0
3x\(^2\)-2x-8=0
3x\(^2\)-6x+4x-8=0
3x(x-2)+4(x-2)=0
(3x+4)(x-2)=0
TH1:3x+4=0 TH2:x-2=0
=>x=\(\dfrac{-4}{3}\) =>x=2
Đúng 0
Bình luận (0)
Bài 8: Tìm giá trị nhỏ nhất của
A=√𝑥2 −4𝑥+25 ,
C=3+√𝑥 √𝑥+1
B=√𝑥2 −6𝑥+30
D=√𝑥2 −4𝑥+7+√2
\(A=\sqrt{x^2-4x+25}=\sqrt{\left(x-2\right)^2+21}\)
Ta có : \(\left(x-2\right)^2\ge0\) => \(\left(x-2\right)^2+21\ge21\left(\forall x\right)\) => \(\sqrt{\left(x-2\right)^2+21}\ge\sqrt{21}\left(\forall x\right)\)
Dấu " = " xảy ra \(\Leftrightarrow\) \(\sqrt{\left(x-2\right)^2}=0\)
\(\Leftrightarrow\) \(x-2=0\)
\(\Leftrightarrow\) x = 2
Vậy giá trị nhỏ nhất của A là : \(\sqrt{21}\) khi x = 2
\(B=\sqrt{x^2-6x+30}=\sqrt{\left(x-3\right)^2+21}\)
Vì \(\sqrt{\left(x-3\right)^2}\ge0\left(\forall x\right)\)=> \(\sqrt{\left(x-3\right)^2+21}\ge\sqrt{21}\left(\forall x\right)\)
Dấu " = " xảy ra \(\Leftrightarrow\) \(\sqrt{\left(x-3\right)^2}=0\)
\(\Leftrightarrow\) \(x-3=0\)
\(\Leftrightarrow\) \(x=3\)
Vậy giá trị nhỏ nhất của B là : \(\sqrt{21}\) khi x = 3
\(D=\sqrt{x^2-4x+7}+\sqrt{2}=\sqrt{\left(x-2\right)^2+3}+\sqrt{2}\)
Vì
e) 𝑥3−3𝑥2−4𝑥+12f) 𝑥3+27+(𝑥+3)(𝑥−9)
phân tích đa thức thành nhân tử
Đúng 0
Bình luận (0)
e) 𝑥3−3𝑥2−4𝑥+12f) 𝑥3+27+(𝑥+3)(𝑥−9)
e) x3-3x2-4x+12
= x2(x-3)-4(x-3)
= (x2-4)(x-3)
Đúng 1
Bình luận (0)