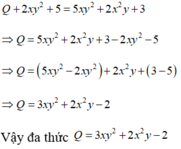P−(3x2y+5xy2+7y)2x2y−12y
Đọc tiếp
P−(3x2y+5xy2+7y)=2x2y−12y
NS
Những câu hỏi liên quan
Cho 2 các đa thức
A= 3x2y+5xy2-2xy+1
B= 2x2y-7xy2+6xy-8
C=-5x2y+4xy2-4xy+12
Tìm x biết A+B+C=0 và y=-2
Ta có: \(A+B+C=0\)
\(\Leftrightarrow3x^2y+5xy^2-2xy+1+2x^2y-7xy^2+6xy-8-5x^2y+4xy^2-4xy+12=0\)
\(\Leftrightarrow2xy^2+5=0\)
\(\Leftrightarrow2x\cdot\left(-2\right)^2+5=0\)
\(\Leftrightarrow8x+5=0\)
\(\Leftrightarrow8x=-5\)
hay \(x=-\dfrac{5}{8}\)
Vậy: \(x=-\dfrac{5}{8}\)
Đúng 1
Bình luận (0)
Thực hiện phép tính và tìm hệ số; biến; bậc của đơn thức thu được a) (2x2y3). (-5/2x2y3)b) (6x2y2z). (1/3xy3)c) 8xy2+5xy2-4xy2d)-1/2x2y+1/3x2y-x2y
Đọc tiếp
Thực hiện phép tính và tìm hệ số; biến; bậc của đơn thức thu được
a) (2x2y3). (-5/2x2y3)
b) (6x2y2z). (1/3xy3)
c) 8xy2+5xy2-4xy2
d)-1/2x2y+1/3x2y-x2y
a: \(=2\cdot\dfrac{-5}{2}\cdot x^2y^3\cdot x^2y^3=-5x^4y^6\)
Hệ số là -5
Biến là x^4;y^6
Bậc là 10
b: \(=6\cdot\dfrac{1}{3}\cdot x^2y^2z\cdot xy^3=2x^3y^5z\)
Hệ số là 2
Biến là x^3;y^5;z
Bậc là 9
c: =xy^2(8+5-4)
=9xy^2
Bậc là 3
Hệ số là 9
Biến là x;y^2
d: =x^2y(-1/2+1/3-1)
=-7/6x^2y
Hệ số là -7/6
Biến là x^2;y
Bậc là 3
Đúng 0
Bình luận (0)
Thu gọn các đa thức ( làm nhanh giúp mình với )
A= 4x2 -3x+7x2+2x-5
B= 3x +7y – 6x – 8 +y – 2
C=4xy -2x2y-xy+3x2y+7
D= 6x4 -3x2 +x2 -4x + 3x4 –x +2
A = \(4x^2-3x+7x^2+2x-5\)
\(11x^2-3x+2x-5\)
\(11x^2-x-5\)
B = \(3x+7y-6x-8+y-2\)
\(3x+7y-6x-10+y\)
\(- 3x+7y-10+y\)
\(3x+8y-10\)
C = chịu
D= \(6x^4-3x^2+x^2-4x+3.4-x+2\)
\(6x^4-3x^2+x^2-4x;12-x+2\\ \)
\(6x^4-3x^2+x^2-4x+14-x\)
\(6x^4-2x^2-4x+14-x\)
\(6x^4-2x^2-5x+14\)
Đúng 1
Bình luận (0)
2x2y;-3x2y;-1/2x2y
Tìm hiệu
P
(
x
)
-
Q
(
x
)
biết
P
(
x
)
(
x
y
2
z
+
3
x
2
y
-
5
x
y
2
)
v
à
Q
(
x
)
(
x...
Đọc tiếp
Tìm hiệu P ( x ) - Q ( x ) biết P ( x ) = ( x y 2 z + 3 x 2 y - 5 x y 2 ) v à Q ( x ) = ( x 2 y + 9 x y 2 z - 5 x y 2 - 3 )
A. - 8 x y 2 z + 2 x 2 y - 3
B. - 8 x y 2 z + 2 x 2 y - 10 x y 2 + 3
C. - 8 x y 2 z - 2 x 2 y + 3
D. - 8 x y 2 z + 2 x 2 y + 3
Ta có: P(x) - Q(x)
= (xy2z + 3x2y - 5xy2)-(x2y + 9xy2z - 5xy2 - 3)
= xy2z + 3x2y - 5xy2 - x2y-9xy2z + 5xy2 + 3
= -8xy2z + 2x2y + 3
Chọn D
Đúng 0
Bình luận (0)
Tổng của các đơn thức
4
x
2
y
,
-
3
x
2
y
,
3
x
2
y
v
à
2
x
2
y
là: A.
6
x
2
y
B.
9
x
2
y
C.
12
x
2...
Đọc tiếp
Tổng của các đơn thức 4 x 2 y , - 3 x 2 y , 3 x 2 y v à 2 x 2 y là:
A. 6 x 2 y
B. 9 x 2 y
C. 12 x 2 y
D. 5 x 2 y
Chọn A
Ta có: 4x2y + (-3x2y) + 3x2y + 2x2y = 6x2y.
Đúng 0
Bình luận (0)
LT
29 tháng 10 2023 lúc 13:50
Thực hiện pt
1/2x2y.(2x3-2/5xy2-1)
\(\dfrac{1}{2}x^2y\left(2x^3-\dfrac{2}{5}xy^2-1\right)\)
\(=\dfrac{1}{2}x^2y\cdot2x^3-\dfrac{1}{2}x^2y\cdot\dfrac{2}{5}xy^2-\dfrac{1}{2}x^2y\)
\(=x^5y-\dfrac{1}{5}x^3y^3-\dfrac{1}{2}x^2y\)
Đúng 2
Bình luận (0)
\(\dfrac{1}{2}x^2y\left(2x^3-\dfrac{2}{5}xy^2-1\right)\)
\(=\dfrac{1}{2}x^2y\cdot2x^3-\dfrac{1}{2}x^2y\cdot\dfrac{2}{5}xy^2-\dfrac{1}{2}x^2y\cdot1\)
\(=x^5y-\dfrac{1}{5}x^3y^3-\dfrac{1}{2}x^2y\)
Đúng 2
Bình luận (0)
Tìm đa thức Q biết
Q
+
2
x
y
2
+
5
5
x
y
2
+
2
x
2
y
+
3
A.
Q
3
x
y
2
...
Đọc tiếp
Tìm đa thức Q biết Q + 2 x y 2 + 5 = 5 x y 2 + 2 x 2 y + 3
A. Q = 3 x y 2 + 2 x 2 y - 2
B. Q = 5 x y 2 + 2 x 2 y - 2
C. Q = 5 x 2 y 2 + 2 x 2 y - 2
D. Q = 5 x y 2 - 2
Tìm số tự nhiên n, biết:
x2y + 2x2y + 3x2y + 4x2y + .... + nx2y = 55x2y
x2y + 2x2y + 3x2y + 4x2y + .... + nx2y = 55x2y
\(\Rightarrow x^2y\left(1+2+...+n\right)=55x^2y\)
\(\Rightarrow1+2+...+n=55\)
\(\Rightarrow\dfrac{\left(\dfrac{n-1}{1}+1\right).\left(n+1\right)}{2}=55\)
\(\Rightarrow n\left(n+1\right)=55.2=110\)
\(\Rightarrow n^2+n-110=0\)
\(\Rightarrow n^2-10n+11n-110=0\)
\(\Rightarrow n\left(n-10\right)+11\left(n-10\right)=0\)
\(\Rightarrow\left(n-10\right)\left(n+11\right)=0\)
\(\Rightarrow n-10=0\) hay \(n+11=0\)
\(\Rightarrow n=10\left(nhận\right)\) hay \(n=-11\left(loại\right)\)
Đúng 2
Bình luận (0)