hộ mik câu 1,2,4,5ko cần câu 3


làm hộ mik câu 3 ( mik đang cần gấp ạ )
\(A=\dfrac{2\sqrt{x}+17}{\sqrt{x+5}}=\dfrac{2\sqrt{x}+10}{\sqrt{x}+5}+\dfrac{7}{\sqrt{x}+5}=2+\dfrac{7}{\sqrt{x}+5}\)
Để \(A\) ∈ \(Z\) thì \(\dfrac{7}{\sqrt{x}+5}\) phải ∈ \(Z\)
=> \(\sqrt{x}+5\) ∈ \(Ư\left(7\right)=\left\{-7;-1;1;7\right\}\)
# Với \(\sqrt{x}+5=-7=>\sqrt{x}=-12\)(Loại)
#Với \(\sqrt{x}+5=-1=>\sqrt{x}=-6\)(Loại)
#Với \(\sqrt{x}+5=1=>\sqrt{x}=-4\left(Loại\right)\)
#Với \(\sqrt{x}+5=7=>\sqrt{x}=2< =>x=4\left(Nhận\right)\)
Vậy \(x=4\) thì \(A\)∈\(Z\)
\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}3\)
\(Ta\) \(Có\) : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}=\sqrt[3]{\dfrac{a^6}{ab.ab\left(a^2-ab+b^2\right)}}=\dfrac{a^2}{\sqrt[3]{ab.ab.\left(a^2-ab+b^2\right)}}\)
\(Áp\) \(dụng\) \(bđt\) \(AM-GM\)
\(\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}\text{≤}\) \(\dfrac{ab+ab+a^2-ab+b^2}{3}\)
\(=>\dfrac{a^2}{\sqrt[3]{ab.ab\left(a^2-ab+b^2\right)}}\) \(\text{≥}\) \(\dfrac{3a^2}{a^2+ab+b^2}\) \(Hay\) \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}\text{≥}\dfrac{3a^2}{a^2+ab+b^2}\)
Tương tự ta cũng có :
\(\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\text{≥}\dfrac{3b^2}{b^2+bc+c^2}\)
\(\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+a^2\right)}}\text{≥}\dfrac{3c^2}{a^2+ac+c^2}\)
\(=>\text{}\text{}\)\(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\)
Cần c/m \(\left(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\right)\) ≥ \(1\)
Ta có : \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
\(< =>3a^2\text{≥}a^2+ab+b^2\) \(< =>2a^2-b\left(a+b\right)\text{≥}0\) (1)
Lại có : \(a^2\text{≥}-b\left(a+b\right)\) (2)
Từ (1) và (2) => \(\dfrac{a^2}{a^2+ab+b^2}\text{≥}\dfrac{1}{3}\)
Tương tự ta cũng có :
\(\dfrac{b^2}{b^2+bc+c^2}\text{≥}\dfrac{1}{3}\)
\(\dfrac{c^2}{a^2+ac+c^2}\text{≥}\dfrac{1}{3}\)
Do đó \(\dfrac{a^2}{a^2+ab+b^2}+\dfrac{b^2}{b^2+bc+c^2}+\dfrac{c^2}{a^2+ac+c^2}\text{≥}1\)
Suy ra : \(\sqrt[3]{\dfrac{a^4}{b^2\left(a^2-ab+b^2\right)}}+\sqrt[3]{\dfrac{b^4}{c^2\left(b^2-bc+c^2\right)}}\sqrt[3]{\dfrac{c^4}{a^2\left(c^2-ac+b^2\right)}}\) \(\text{≥}\) \(3\)
Đẳng thức xảy ra <=> \(a=b=c=1\)
Giải hộ mik câu 18 nhé! Mik cần gấp
= \(\left(6-\dfrac{14}{5}\right).\dfrac{25}{8}-\dfrac{8}{5}:\dfrac{1}{4}\)
= \(\dfrac{16}{5}.\dfrac{25}{8}-\dfrac{32}{5}\)
=10-\(\dfrac{32}{5}\)
=\(\dfrac{18}{5}\)
\(\left(6-2\dfrac{4}{5}\right).3\dfrac{1}{8}-1\dfrac{3}{5}:\dfrac{1}{4}\) \(=\left(6-\dfrac{14}{5}\right).\dfrac{25}{8}-\dfrac{8}{5}:\dfrac{1}{4}\)
\(=\dfrac{16}{5}.\dfrac{25}{8}-\dfrac{8}{5}:\dfrac{1}{4}\)
\(=10-\dfrac{32}{5}\)
\(=\dfrac{50}{5}-\dfrac{32}{5}\)
\(=\dfrac{18}{5}\)
làm hộ mik câu b,c mik cần gấp
a: Thay a=-2 vào pt, ta được:
\(-2x^2-2\cdot\left(-2-1\right)x-2+1=0\)
\(\Leftrightarrow-2x^2+6x-1=0\)
\(\Leftrightarrow2x^2-6x+1=0\)
\(\text{Δ}=\left(-6\right)^2-4\cdot2\cdot1=36-8=28>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{6-2\sqrt{7}}{2}=3-\sqrt{7}\\x_2=3+\sqrt{7}\end{matrix}\right.\)
b: Để phương trình có hai nghiệm phân biệt thì
\(\left\{{}\begin{matrix}\left(-2a+2\right)^2-4a\left(a+1\right)>0\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a^2-8a+4-4a^2-4a>0\\a< >0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-12a>-4\\a< >0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a< >0\\a< \dfrac{1}{3}\end{matrix}\right.\)

giải hộ mik câu 15,16,17 vs ạ mik đang cần gấp
15:
a: \(\text{Δ}=\left(m^2-m+2\right)^2-4m^2\)
=(m^2-m+2-2m)(m^2-m+2+2m)
=(m^2+m+2)(m^2-3m+2)
=(m-1)(m-2)(m^2+m+2)
Để phương trình co hai nghiệm phân biệt thì (m-1)(m-2)(m^2+m+2)>0
=>(m-1)(m-2)>0
=>m>2 hoặc m<1
b: x1+x2=m^2-m+2>0 với mọi m
x1*x2=m^2>0 vơi mọi m
=>Phương trình luôn có hai nghiệm dương phân biệt
Ai trl hộ mik câu 6 với ạ cô ?
Mik cần gấp ://
Ai giải hộ mik câu 4 với mik đang cần rất gấp ạ !!!!!!
- Tương phản khi một vị quan phụ mẫu quyền cao chức trọng đang ngồi chơi bài trong một cái đình cao ráo, cùng với bao của ngon vật lạ, trong khi đó hàng bao người dân đang vất vả ngăn lại con lũ dữ dội bên ngoài kia
=> Tác dụng: Việc sử dụng 2 hình ảnh tương phản này góp phần nhấn mạnh thêm vào 2 điều:
1. Đời sống khổ cực của nhân dân, chịu những thiên tai dữ dội nhưng lại phải tự lo, không được sự trợ giúp của vị quan phụ mẫu
2. Sự vô tâm, không làm tròn trách nhiệm của lão quan phụ mẫu, hút máu nhân dân để sống mà không quan tâm đến nỗi khổ nhân dân, chỉ lo hưởng thụ cuộc sống giàu sang, sung túc, ăn chơi
P/s: Vì chị lớp 9 rồi nên không dám đảm bảo nhớ đúng từng chi tiết, nhưng đại ý nó là thế này
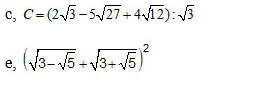
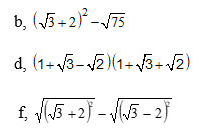 các bạn giải hộ mik mấy câu này vs mik đag cần gấp
các bạn giải hộ mik mấy câu này vs mik đag cần gấp
c, \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
<=> \(C=\left(2\sqrt{3}-15\sqrt{3}+8\sqrt{3}\right):\sqrt{3}\)
<=> \(C=-5\sqrt{3}:\sqrt{3}=-5\)
e. \(\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\sqrt{9-5}\)
\(=6+4=10\)
b. \(\left(\sqrt{3}+2\right)^2-\sqrt{75}\)
\(=3+4\sqrt{3}+4-5\sqrt{3}\)
\(=7-\sqrt{3}\)
d. \(\left(1+\sqrt{3}-\sqrt{2}\right)\left(1+\sqrt{3}+\sqrt{2}\right)\)
\(=\left(1+\sqrt{3}\right)^2-2\)
\(=1+2\sqrt{3}+3-2\)
\(=2+2\sqrt{3}\)
f. \(\sqrt{\left(\sqrt{3}+2\right)^2}-\sqrt{\left(\sqrt{3}-2\right)^2}\)
\(=\left|\sqrt{3}+2\right|-\left|\sqrt{3}-2\right|\)
\(=\sqrt{3}+2-2+\sqrt{3}\)
\(=2\sqrt{3}\)
c: Ta có: \(C=\left(2\sqrt{3}-5\sqrt{27}+4\sqrt{12}\right):\sqrt{3}\)
\(=\left(2\sqrt{3}-5\cdot3\sqrt{3}+4\cdot2\sqrt{3}\right):\sqrt{3}\)
\(=2-15+8=-5\)
d: Ta có: \(D=\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)^2\)
\(=3-\sqrt{5}+3+\sqrt{5}+2\cdot\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\)
\(=6+2\cdot2=10\)
làm hộ mik câu 1.2, 2.2(CÂU NÀY LÀM BẰNG PP CHẶN GIÚP MIK Ạ) , 3.2 nha
MIK CẢM ƠN Ạ
MIK ĐANG CẦN RẤT GẤP NÊN MỌI NGƯỜI GIÚP MIK Ạ

1.2 với \(x\ge0,x\in Z\)
A=\(\dfrac{2\sqrt{x}+7}{\sqrt{x}+2}=2+\dfrac{3}{\sqrt{x}+2}\in Z< =>\sqrt{x}+2\inƯ\left(3\right)=\left(\pm1;\pm3\right)\)
*\(\sqrt{x}+2=1=>\sqrt{x}=-1\)(vô lí)
*\(\sqrt{x}+2=-1=>\sqrt{x}=-3\)(vô lí
*\(\sqrt{x}+2=3=>x=1\)(TM)
*\(\sqrt{x}+2=-3=\sqrt{x}=-5\)(vô lí)
vậy x=1 thì A\(\in Z\)
viết 2 - 3 câu nêu cảm nghĩ của em sau khi đọc bài thơ CHỢ TẾT ?
trl hộ mik nhanh lên nhá mik đang cần gấp
Tham khảo
Bức tranh dân gian "Chợ Tết" của Đoàn Văn Cừ mang vẻ đẹp vừa bình dị thân thuộc, vừa rực rỡ sắc màu. Tác giả đã làm sống lại cảnh vật và cuộc sống nơi đồng quê đậm đà màu sắc văn hóa dân gian với tất cả tấm lòng yêu thương nồng hậu.
Tham khảo :
Mỗi người đi chợ Tết đều có một dáng vẻ riêng. Đoàn Văn Cừ đã làm hiện lên trước mắt chúng ta những con người hiền lành, giản dị, đáng yêu bằng bao nét vẽ có hồn, rất sinh động. Mặc áo đỏ, áo mới, áo đẹp là những thằng cu "chạy lon xon" mừng vui tíu tít. Là vài cụ già, tay chống gậy, lung còng "bước lom khom" chậm rãi. Là cô thôn nữ xinh tươi với chiếc yếm thắm, duyên dáng và kín đáo "che môi cười lặng lẽ". Là những em bé lần đầu được đi chợ Tết, còn rụt rè sợ hãi "nép đầu bên yếm mẹ?"...ngơ ngác trước những con người lạ, cảnh lạ:
Tham khảo
Bức tranh dân gian "Chợ Tết" của Đoàn Văn Cừ mang vẻ đẹp vừa bình dị thân thuộc, vừa rực rỡ sắc màu. Tác giả đã làm sống lại cảnh vật và cuộc sống nơi đồng quê đậm đà màu sắc văn hóa dân gian với tất cả tấm lòng yêu thương nồng hậu.